Решебник по геометрии 10 класс Атанасян ФГОС 304

\[\boxed{\mathbf{304.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

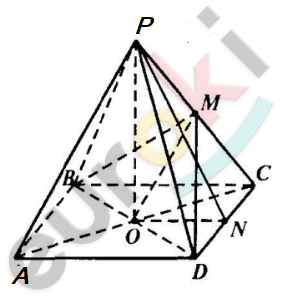
\[Доказательство.\]

\[1)\ Рассмотрим\ пирамиду\ \]

\[\text{PABCD.\ }\]

\[O\ —\ точка\ пересечения\ \]

\[диагоналей\ квадрата\ ABCD.\ \]

\[M\ —\ середина\ PC;\ \ \ \]

\[N\ —\ середина\ CD.\]

\[2)\ \ \angle CPD\ = \ 60{^\circ}:\]

\[равнобедренный\ треугольник\ \]

\[CPD\ является - \ \]

\[равносторонним.\ \]

\[Все\ ребра\ пирамиды\ равны\ \]

\[между\ собой:\ \]

\[BM = MD;\]

\[медиана\ MO\ является\ \]

\[биссектрисой\ \Delta BMD.\]

\[3)\ PN\ = \ MD\ —\ как\ медианы\ \]

\[равностороннего\ \Delta DPC.\]

\[NO = \frac{1}{2}AD;\ \ MO = \frac{1}{2}AP - как\ \]

\[средние\ линии\ ⊿CAD\ и\ ⊿CPA:\]

\[NO = MO.\]

\[Тогда:\]

\[⊿DMO = ⊿PNO - по\ катету\ и\ \]

\[гипотенузе.\]

\[Значит:\]

\[\angle PNO = \angle DMO = \frac{1}{2}\angle DMB.\]

\[\angle PNO\ —\ угол\ между\ боковой\ \]

\[гранью\ и\ основанием;\]

\[\angle DMB\ —\ линейный\ угол\ \]

\[двугранного\ угла\ при\ боковом\ \]

\[ребре.\ \]

\[Что\ и\ требовалось\ доказать.\]