Решебник по геометрии 10 класс Атанасян ФГОС 29

\[\boxed{\mathbf{29.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[ABCD - трапеция;\]

\[BC \parallel AD;\]

\[BC = 12\ см;\]

\[M \notin ABCD;\]

\[BK = KM.\]

\[Доказать:\]

\[ADK \cap MC = H.\]

\[Найти:\]

\[\text{KH.}\]

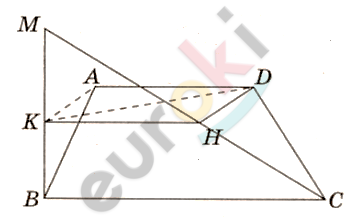
\[Решение.\]

\[1)\ AD = ABCD \cap ADK.\]

\[Теорема:\ \]

\[если\ прямая,\ не\ лежащая\ в\ \]

\[данной\ плоскости,\ \]

\[параллельна\ какой - нибудь\ \]

\[прямой,\ лежащей\ в\ этой\ \]

\[плоскости,\ то\ она\ параллельна\ \]

\[данной\ плоскости.\]

\[2)\ ABCD - трапеция:\]

\[AD \parallel BC.\]

\[Следовательно:\]

\[BC \subset BMC;\]

\[AD \parallel BMC.\]

\[3)\ KN \parallel AD - пересечение\ \]

\[плоскостей\ \text{BMC\ }и\ ADK:\]

\[AD \parallel BMC;\]

\[\text{AD} \in ADK;\]

\[\text{ADK} \cap BMC = K.\]

\[4)\ По\ теореме\ о\ \]

\[пропорциональных\ отрезках\ \]

\[\left( в\ плоскости\ \text{BMC} \right):\]

\[H - середина\ MC;\]

\[KH - средняя\ линия\ ⊿BMC;\]

\[KH = 6\ см.\]

\[Ответ:6\ см.\]