Решебник по геометрии 10 класс Атанасян ФГОС 27

\[\boxed{\mathbf{27.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[AB\ :BC = 4\ :3\]

\[C \in AB;B \in \alpha;\]

\[CD \parallel \alpha;\]

\[CD = 12\ см.\]

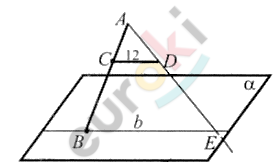
\[Доказать:\]

\[AD \cap \alpha = E.\]

\[Найти:\]

\[DE - ?\]

\[Решение.\]

\[Плоскости\ \text{ABE\ }и\ \alpha\ \]

\[пересекаются,\ то\ \]

\[BE = ABD \cap \alpha.\]

\[Если\ плоскость\ проходит\ через\ \]

\[данную\ прямую,\ параллельную\]

\[другой\ плоскости\ и\ \]

\[пересекающую\ эту\ плоскость,\ \]

\[то\ линия\ пересечения\ \]

\[плоскостей\ параллельна\ \]

\[данной\ прямой.\]

\[E = AD \cap \alpha \rightarrow CD \parallel BE.\]

\[В\ плоскости\ BAE:\]

\[⊿BAE;\]

\[CD \parallel BE.\]

\[Из\ курса\ планиметрии:\]

\[если\ пересечь\ треугольник\ \]

\[прямой,\ параллельной\ \]

\[основанию,\ то\]

\[полученные\ треугольники\ \]

\[подобны:\]

\[⊿BAE\sim ⊿CAD.\]

\[Коэффициент\ подобия\ равен\ 4:\]

\[4 = \frac{3 \cdot x + x}{x}\]

\[BE = 4 \cdot CD = 48\ см.\]

\[Ответ:48\ см.\]