Решебник по геометрии 10 класс Атанасян ФГОС 194

\[\boxed{\mathbf{194.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[\text{ABCD}A_{1}B_{1}C_{1}D_{1} - куб\ со\ \]

\[стороной\ \text{a.}\]

\[Найти:\]

\[расстояние\ между\]

\[\textbf{а)}\ диагональ\ куба\ и\ ребро\ куба;\]

\[\textbf{б)}\ диагональ\ куба\ и\ диагональ\ \]

\[грани\ куба.\]

\[Решение.\]

\[\textbf{а)}\]

\[Расстояние\ от\ прямой\ AA_{1}\ до\ \]

\[прямой\ B_{1}\text{D\ }равно\ AO:\]

\[AA_{1} \parallel DD_{1};\ \ AA_{1} \parallel BB_{1};\]

\[O - середина\ \text{BD\ }и\ \text{AC.}\]

\[AO\bot BD;\ \ AO\bot DD_{1}:\]

\[AO\bot BB_{1}D_{1}D;\]

\[AO = \frac{1}{2}\text{AC.}\]

\[По\ теореме\ Пифагора:\]

\[AC = \sqrt{AD^{2} + CD^{2}} =\]

\[= \sqrt{a^{2} + a^{2}} = a\sqrt{2}.\]

\[AO = \frac{a\sqrt{2}}{2}\text{\ .}\]

\[Ответ:\ \frac{a\sqrt{2}}{2}\text{\ .}\]

\[\textbf{б)}\ OK \parallel B_{1}\text{D.}\]

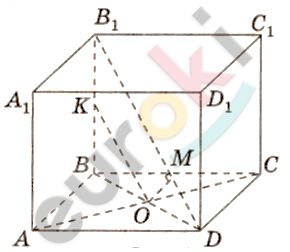
\[В\ треугольнике\ BB_{1}D:\]

\[KO - средняя\ линия;\]

\[OM - расстояние\ между\ \]

\[диагональю\ куба\ и\ диагональю\ \]

\[грани\ куба.\]

\[По\ теореме\ Пифагора:\]

\[B_{1}D = \sqrt{BB_{1}^{2} + BD^{2}} =\]

\[= \sqrt{a^{2} + \left( a\sqrt{2} \right)^{2}} = a\sqrt{3}.\]

\[По\ определению\ синуса:\]

\[\sin{\angle B_{1}\text{DB}} = \frac{BB_{1}}{B_{1}D} = \frac{a}{a\sqrt{3}} = \frac{1}{\sqrt{3}}.\]

\[В\ треугольнике\ MDO:\]

\[\sin{\angle MDO} = OM\ :\frac{a\sqrt{2}}{2} =\]

\[= \frac{\sqrt{2} \cdot OM}{a};\]

\[\sin{\angle B_{1}\text{DB}} = \sin{\angle MDO}\]

\[\frac{1}{\sqrt{3}} = \frac{\sqrt{2} \cdot OM}{a}\]

\[OM = \frac{a\sqrt{6}}{6}\text{\ .}\]

\[Ответ:\ \ \frac{a\sqrt{6}}{6}\text{\ .}\]