Решебник по геометрии 10 класс Атанасян ФГОС 155

\[\boxed{\mathbf{155.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[\mathrm{\Delta}ABC;\]

\[\angle C = 90{^\circ};\]

\[AC = BC;\]

\[CM\bot ABC;\]

\[AC = 4\ см;\]

\[CM = 2\sqrt{7}\ см.\]

\[Найти:\]

\[p(M,AB).\]

\[Решение.\]

\[1)\ Пусть\ MK = p(M,AB):\]

\[MK\bot AB.\]

\[2)\ Так\ как\ AC\bot ABC:\ \ \]

\[MK - наклонная\ к\ ABC,\ \]

\[KC - проекция\ MK\ на\ ABC,\ \]

\[MK\bot AB.\]

\[Следовательно:\]

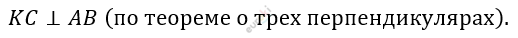
\[3)\ Рассмотрим\ \mathrm{\Delta}ABC:\]

\[KC\bot AB;\]

\[KC - высота\ \mathrm{\Delta}ABC;\]

\[AC = CB.\]

\[Значит:\]

\[KC - медина\ \mathrm{\Delta}ABC;\]

\[AK = KB;\]

\[AC = CB.\ \]

\[Следовательно:\ \]

\[\angle A = \angle B = 45{^\circ}.\]

\[4)\ \mathrm{\Delta}AKC - прямоугольный:\]

\[\angle K = 90{^\circ};\ \]

\[\angle A = 45{^\circ}.\]

\[Значит:\ \]

\[\angle C = 180{^\circ} - 90{^\circ} - 45{^\circ} = 45{^\circ};\]

\[\mathrm{\Delta}AKC - равнобедренный.\]

\[Отсюда:\ \]

\[AK = KC = AC \bullet \cos{45{^\circ}} =\]

\[= \frac{AC \bullet \sqrt{2}}{2} = \frac{4\sqrt{2}}{2} = 2\sqrt{2}\ см.\]

\[5)\ \mathrm{\Delta}MKC - прямоугольный:\]

\[MK = \sqrt{MC^{2} + KC^{2}} =\]

\[= \sqrt{2{\sqrt{7}}^{2} + 2{\sqrt{2}}^{2}} = \sqrt{4 \bullet 9} =\]

\[= 6\ см.\]

\[Ответ:p(M,AB) = 6\ см.\]