Решебник по геометрии 10 класс Атанасян ФГОС 125

\[\boxed{\mathbf{125.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[PP_{1} \cap \alpha = P_{1};\]

\[QQ_{1} \cap \alpha = Q_{1};\]

\[PP_{1}\bot\alpha;\]

\[QQ_{1}\bot\alpha;\]

\[PQ = 15\ см;\]

\[PP_{1} = 21,5\ см;\]

\[QQ_{1} = 33,5\ см.\]

\[Найти:\]

\[P_{1}Q_{1}.\]

\[Решение.\]

\[1)\ PP_{1}\bot\alpha\ и\ QQ_{1}\bot\alpha:\]

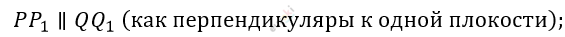
\[PP_{1}\ и\ QQ_{1}\ принадлежат\ к\ \]

\[одной\ плоскости\ P_{1}Q_{1}PQ;\]

\[\alpha \cap P_{1}Q_{1}QP = P_{1}Q_{1}.\]

\[2)\ P_{1}Q_{1}PQ - трапеция:\]

\[PP_{1} \parallel QQ_{1}.\]

\[3)\ Проведем\ высоту\ \text{T.}\]

\[4)\ PTP_{1}Q_{1} - прямоугольник:\]

\[\angle P_{1} = \angle Q_{1} = \angle T = 90{^\circ};\ \]

\[\angle P = 90{^\circ}\ \]

\[(по\ теореме\ о\ сумме\ углов).\]

\[Отсюда:\ \]

\[PT = P_{1}Q_{1};\]

\[TQ_{1} = PP_{1} = 21,5\ см.\]

\[5)\ \mathrm{\Delta}TPQ - прямоугольный:\]

\[QT = QQ_{1} - TQ_{1} =\]

\[= 33,5 - 21,5 = 12\ см;\]

\[PT = P_{1}Q_{1} = \sqrt{15^{2} - 12^{2}} =\]

\[= \sqrt{81} = 9\ см.\]

\[Ответ:9\ см.\]