Решебник по алгебре 9 класс Макарычев Задание 886

 

\[\boxed{\text{886}\text{\ (886)}\text{.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ 3x^{2} - 6x - 5\ \ \ \ \]

\[при\ x = 1 + \sqrt{2}:\]

\[3x^{2} - 6x - 5 =\]

\[= 3 \cdot \left( 1 + \sqrt{2} \right)^{2} - 6 \cdot \left( 1 + \sqrt{2} \right) - 5 =\]

\[= 3 + 6\sqrt{2} + 6 - 6 - 6\sqrt{2} - 5 =\]

\[= - 2.\]

\[\textbf{б)}\ \frac{x^{2} - x - 5}{x - 1}\]

\[при\ x = \sqrt{5} + 1:\]

\[\frac{x^{2} - x - 5}{x - 1} =\]

\[= \frac{\left( \sqrt{5} + 1 \right)^{2} - \left( \sqrt{5} + 1 \right) - 5}{\sqrt{5} + 1 - 1} =\]

\[= \frac{5 + 2\sqrt{5} + 1 - \sqrt{5} - 1 - 5}{\sqrt{5}} =\]

\[= \frac{\sqrt{5}}{\sqrt{5}} = 1.\]

\[\boxed{\text{886.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[Пусть\ x - одно\ число,\ тогда\ \]

\[y - второе\ число.\ По\ условию,\ \]

\[x > y.\]

\[x + y + xy + x - y + \frac{x}{y} = 441\]

\[2x + xy + \frac{x}{y} = 441\ \]

\[\frac{2xy + xy^{2} + x}{y} = 441\]

\[\frac{x}{y} \cdot \left( y^{2} + 2y + 1 \right) = 441\]

\[\frac{x}{y} \cdot (y + 1)^{2} = 21^{2}\]

\[\frac{x}{y} \Longrightarrow натуральное\ число\ \ \]

\[(по\ условию).\]

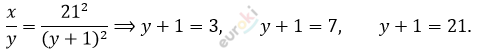
\[1)\ y + 1 = 3,\ \ y = 2,\]

\[\frac{x}{y} = 49 \Longrightarrow x = 98,\]

\[2)\ y + 1 = 7,\ \ y = 6,\]

\[\frac{x}{y} = 9 \Longrightarrow x = 54,\]

\[3)\ y + 1 = 21,\ \ y = 20,\]

\[\frac{x}{y} = 1 \Longrightarrow x = 20 \Longrightarrow\]

\[\Longrightarrow не\ подходит\ по\ условию\ \]

\[(x > y).\]

\[Ответ:(98;2);\ \ (54;6).\]