Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Макарычев Задание 871
Задание 871
\[\boxed{\text{871\ (871).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[Найдем,\ чему\ равна\ \]
\[вероятность\ того,\ что\ наберут\ \]
\[одну\ правильную\ цифру\ из\ 10:\ \ \]
\[P = \frac{1}{10}.\]
\[Найдем,\ чему\ равна\ \]
\[вероятность\ того,\ что\ наберут\ \]
\[5\ правильных\ цифр:\ \]
\[P = \left( \frac{1}{10} \right)^{5} = 0,00001.\]
\[Ответ:0,00001.\]
\[\boxed{\text{871.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]
\[x_{n} = \frac{1}{\sqrt{a_{n}} + \sqrt{a_{n + 1}}},\ \ \]
\[S_{n} = \frac{n}{\sqrt{a_{1}} + \sqrt{a_{n + 1}}},\]
\[x_{n} = \frac{1}{\sqrt{a_{n}} + \sqrt{a_{n + 1}}} =\]
\[= \frac{\sqrt{a_{n + 1}} - \sqrt{a_{n}}}{\left( \sqrt{a_{n}} + \sqrt{a_{n + 1}} \right)\left( \sqrt{a_{n + 1}} - \sqrt{a_{n}} \right)} =\]
\[= \frac{\sqrt{a_{n + 1}} - \sqrt{a_{n}}}{a_{n + 1} - a_{n}} =\]
\[= \frac{\sqrt{a_{n + 1}} - \sqrt{a_{n}}}{d}.\]
\[x_{1} = \frac{\sqrt{a_{2}} - \sqrt{a_{1}}}{d},\]
\[x_{2} = \frac{\sqrt{a_{3}} - \sqrt{a_{2}}}{d},\]
\[x_{n - 1} = \frac{\sqrt{a_{n}} - \sqrt{a_{n - 1}}}{d},\]
\[x_{n} = \frac{\sqrt{a_{n + 1}} - \sqrt{a_{n}}}{d}.\]
\[S_{n} = x_{1} + x_{2} + \ldots + x_{n - 1} + x_{n} =\]
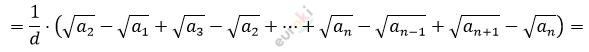
\[= \frac{1}{d} \cdot \left( \sqrt{a_{n + 1}} - \sqrt{a_{1}} \right) =\]
\[= \frac{\left( \sqrt{a_{n + 1}} - \sqrt{a_{1}} \right)\left( \sqrt{a_{n + 1}} + \sqrt{a_{1}} \right)}{d\left( \sqrt{a_{n + 1}} + \sqrt{a_{1}} \right)} =\]
\[= \frac{a_{n + 1} - a_{1}}{d\left( \sqrt{a_{n + 1}} + \sqrt{a_{1}} \right)} =\]
\[= \frac{a_{1} + nd - a_{1}}{d\left( \sqrt{a_{n + 1}} + \sqrt{a_{1}} \right)} =\]
\[= \frac{n}{\sqrt{a_{1}} + \sqrt{a_{n + 1}}} \Longrightarrow ч.т.д.\]
