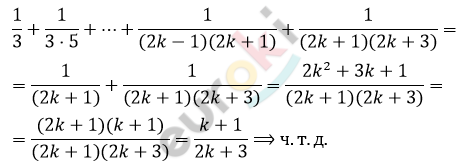Решебник по алгебре 9 класс Макарычев Задание 867

\[\boxed{\text{867\ (867).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\frac{n}{12} = \frac{1}{6}\]

\[6n = 12\]

\[n = 2.\]

\[Ответ:2\ белых\ шара\ в\ коробке.\]

\[\boxed{\text{867.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[x_{n} = \frac{1}{(2n - 1)(2n + 1)};\ \ \]

\[x_{1} = \frac{1}{3},\ \ x_{2} = \frac{1}{3 \cdot 5},\ \ \]

\[x_{3} = \frac{1}{5 \cdot 7}.\]

\[Докажем,\ что\ искомая\ сумма\ \]

\[может\ быть\ найдена\ \]

\[по\ формуле:\]

\[S_{n} = \frac{n}{2n + 1}.\]

\[Предположим,\ что\ формула\ \]

\[верна\ для\ n = k.\ Докажем,\ что\ \]

\[она\ верна\ для\ n = k + 1:\]