Решебник по алгебре 9 класс Макарычев Задание 798

 

\[\boxed{\text{798\ (798).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Найдем,\ какова\ вероятность\ \]

\[того,\ что\ купленный\ билет\ \]

\[окажется\ выигрышным:\ \ \]

\[\frac{120}{1500} = 0,08.\]

\[\boxed{\text{798.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[\textbf{а)}\ 0,3 \cdot (2m - 3) < 3 \cdot (0,6m + 1,3)\]

\[0,6m - 0,9 < 1,8m + 3,9\]

\[1,2m > - 4,8\]

\[m > - 4.\]

\[\textbf{б)}\ 1,1 \cdot (5x - 4) > 0,2 \cdot (10x - 43)\]

\[5,5x - 4,4 > 2x - 8,6\]

\[3,5x > - 4,2\]

\[x > - 1,2.\]

\[\textbf{в)}\ 10 - 5 \cdot (0,3a - 0,2) \geq\]

\[\geq 5 - 10 \cdot (0,1a + 0,2)\]

\[10 - 1,5a + 1 \geq 5 - a - 2\]

\[0,5a \leq 8\]

\[a \leq 16.\]

\[\textbf{г)}\ 3,2 \cdot (2b + 1) + 5,7 \leq\]

\[\leq 7,3 - 1,6 \cdot (3 - 5b)\]

\[6,4b + 3,2 + 5,7 \leq 7,3 - 4,8 + 8b\]

\[1,6b \geq 6,4\]

\[b \geq 4.\]

\[\textbf{д)}\ 4,3x - \frac{1}{2} \cdot (2,8x - 0,6) >\]

\[> \frac{1}{3} \cdot (3x + 0,6) + 2,9x\]

\[4,3x - 1,4x + 0,3 > x + 0,2 + 2,9x\]

\[3,9x - 2,9x < 0,3 - 0,2\]

\[x < 0,1.\]

\[\textbf{е)}\frac{2}{5} \cdot (5,5m - 2) - 0,8m <\]

\[< 4,6m - \frac{3}{4} \cdot (3,6m - 1,6)\]

\[2,2m - 0,8 - 0,8m <\]

\[< 4,6m - 2,7m + 1,2\]

\[1,9m - 1,4m > - 0,8 - 1,2\]

\[0,5m > - 2\]

\[m > - 4.\]

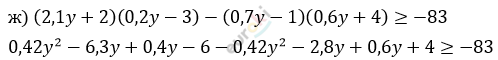
\[- 8,1 \geq - 83 + 2\]

\[8,1y \leq 81\]

\[y \leq 10.\]

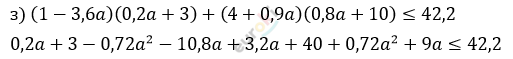
\[1,6a \leq 42,2 - 43\]

\[1,6a \leq - 0,8\]

\[a \leq - 0,5.\]