Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Макарычев Задание 710
Задание 710
\[\boxed{\text{710\ (710).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\textbf{а)}\ q = - \frac{1}{3},\ \ n = 5,\ \ \]
\[S_{n} = 20\frac{1}{3},\]
\[x_{1} = ?,\ \ x_{n} = ?\]
\[S_{5} = x_{1} \cdot \frac{q^{5} - 1}{q - 1}\]
\[x_{1} \cdot \frac{\left( - \frac{1}{3} \right)^{5} - 1}{- \frac{1}{3} - 1\ } = 20\frac{1}{3}\]
\[x_{1} = \frac{- \frac{1}{243} - 1}{- \frac{4}{3}} = \frac{61}{3}\]
\[x_{1} \cdot \frac{244}{243} \cdot \frac{3}{4} = \frac{61}{3}\]
\[x_{1} = \frac{61}{3} \cdot \frac{81}{61}\]
\[x_{5} = x_{1} \cdot q^{4} = 24 \cdot \frac{1}{3^{4}}\]
\[\textbf{б)}\ x_{1} = 11,\ \ x_{n} = 88,\ \ \]
\[S_{n} = 165,\]
\[q = ?,\ \ n = ?\]
\[x_{n} = x_{1} \cdot q^{n - 1} = 88,\]
\[q^{n - 1} = \frac{88}{11} = 8,\]
\[S_{n - 1} = x_{1} \cdot \frac{q^{n - 1} - 1}{q - 1} = S_{n} - x_{n}\]
\[11 \cdot \frac{q^{n - 1} - 1}{q - 1} = 165 - 88\]
\[\frac{77}{q - 1} = 77\]
\[x_{n} = x_{1} \cdot q^{n - 1}\]
\[88 = 11 \cdot 2^{n - 1}\]
\[2^{n - 1} = 8\]
\[n - 1 = 3\]
\[\textbf{в)}\ x_{1} = \frac{1}{2},\ \ q = - \frac{1}{2},\ \ \]
\[S_{n} = \frac{21}{64},\]
\[n = ?,\ \ x_{n} = ?\]
\[S_{n} = x_{1} \cdot \frac{q^{n} - 1}{q - 1},\]
\[\frac{21}{64} = \frac{1}{2} \cdot \frac{\left( - \frac{1}{2} \right)^{n} - 1}{- \frac{1}{2} - 1},\]
\[\frac{21}{32} = \frac{\left( - \frac{1}{2} \right)^{n} - 1}{- \frac{3}{2}},\]
\[- \frac{63}{64} = \left( - \frac{1}{2} \right)^{n} - 1\]
\[\left( - \frac{1}{2} \right)^{n} = \frac{1}{64}\]
\[x_{6} = x_{1} \cdot q^{5} = \frac{1}{2} \cdot \left( - \frac{1}{2} \right)^{5}\]
\[\textbf{г)}\ q = \sqrt{3},\ \ x_{n} = 18\sqrt{3},\ \ \]
\[S_{n} = 26\sqrt{3} + 24,\]
\[x_{1} = ?,\ \ n = ?\]
\[S_{n} = x_{1} \cdot \frac{q^{n} - 1}{q - 1} = 26\sqrt{3} + 24\]
\[\frac{18\sqrt{3} \cdot \sqrt{3} - x_{1}}{\sqrt{3} - 1} = 26\sqrt{3} + 24\]
\[54 - x_{1} = \left( 26\sqrt{3} + 24 \right)\left( \sqrt{3} - 1 \right)\]
\[54 - x_{1} =\]
\[= 26 \cdot 3 - 26\sqrt{3} + 24\sqrt{3} - 24\]
\[18\sqrt{3} = 2\sqrt{3} \cdot \left( \sqrt{3} \right)^{n - 1}\]
\[\left( \sqrt{3} \right)^{n - 1} = 9\]
\[n - 1 = 4\]
\[\boxed{\text{710.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]
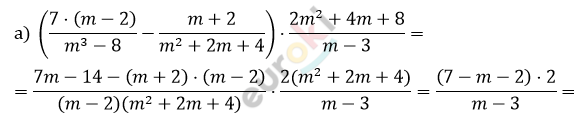
\[= \frac{10 - 2m}{m - 3}\]
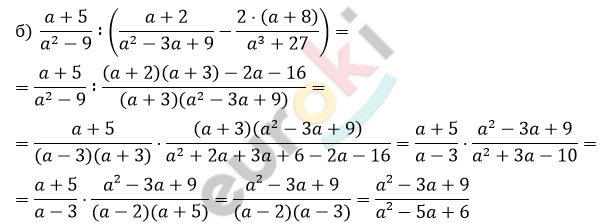
\[a^{2} + 3a - 10 = (a - 2)(a + 5)\]
\[x_{1} + x_{2} = - 3;\ \ \ \ x_{1} \cdot x_{2} = - 10\]
\[x_{1} = 2;\ \ \ \ x_{2} = - 5.\]
\[= \frac{2 \cdot (x - 5)(x - 2)}{(x - 2)(x + 2)(x - 5)} =\]
\[= \frac{2}{x + 2}\]
\[2x^{2} - 14x + 20 =\]
\[= (x - 5)(x - 2)\]
\[D = 196 - 160 = 36\]
\[x_{1} = 5,\ \ x_{2} = 2.\]
