Решебник по алгебре 9 класс Макарычев Задание 670

 

\[\boxed{\text{670}\text{\ (670)}\text{.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ c_{n} = - 2n^{2} + 7\]

\[c_{1} = - 2 \cdot 1^{2} + 7 = 5\]

\[c_{2} = - 2 \cdot 2^{2} + 7 = - 1\]

\[c_{3} = - 2 \cdot 3^{2} + 7 = - 11\]

\[c_{4} = - 2 \cdot 4^{2} + 7 = - 25\]

\[c_{5} = - 2 \cdot 5^{2} + 7 = - 43.\]

\[\textbf{б)}\ c_{n} = \frac{100}{n² - 5}\]

\[c_{1} = \frac{100}{1^{2} - 5} = - 25\]

\[c_{2} = \frac{100}{2² - 5} = - 100\]

\[c_{3} = \frac{100}{3² - 5} = 25\]

\[c_{4} = \frac{100}{4² - 5} = \frac{100}{11} = 9\frac{1}{11}\]

\[c_{5} = \frac{100}{5² - 5} = 5.\]

\[\textbf{в)}\ c_{n} = - 2,5 \cdot 2^{n}\]

\[c_{1} = - 2,5 \cdot 2^{1} = - 5\]

\[c_{2} = - 2,5 \cdot 2^{2} = - 10\]

\[c_{3} = - 2,5 \cdot 2^{3} = - 20\]

\[c_{4} = - 2,5 \cdot 2^{4} = - 40\]

\[c_{5} = - 2,5 \cdot 2^{5} = - 80.\]

\[\textbf{г)}\ c_{n} = 3,2 \cdot 2^{- n}\]

\[c_{1} = 3,2 \cdot 2^{- 1} = 1,6\]

\[c_{2} = 3,2 \cdot 2^{- 2} = 0,8\]

\[c_{3} = 3,2 \cdot 2^{- 3} = 0,4\]

\[c_{4} = 3,2 \cdot 2^{- 4} = 0,2\]

\[c^{5} = 3,2 \cdot 2^{- 5} = 0,1.\]

\[\textbf{д)}\ c_{n} = \frac{( - 1)^{n - 1}}{4n}\]

\[c_{1} = \frac{( - 1)^{0}}{4} = \frac{1}{4}\]

\[c_{2} = \ \frac{( - 1)^{1}}{4 \cdot 2} = - \frac{1}{8}\]

\[c_{3} = \frac{( - 1)²}{4 \cdot 3} = \frac{1}{12}\]

\[c_{4} = \frac{( - 1)³}{4 \cdot 4} = - \frac{1}{16}\]

\[c_{5} = \frac{( - 1)^{4}}{4 \cdot 5} = \frac{1}{20}.\]

\[\textbf{е)}\ c_{n} = \frac{1 - ( - 1)^{n}}{2n + 1}\]

\[c_{1} = \frac{1 - ( - 1)}{2 + 1} = \frac{2}{3}\]

\[c_{2} = \ \frac{1 - ( - 1)²}{2 \cdot 2 + 1} = 0\]

\[c_{3} = \frac{1 - ( - 1)³}{2 \cdot 3 + 1} = \frac{2}{7}\]

\[c_{4} = \frac{1 - ( - 1)^{4}}{2 \cdot 4 + 1} = 0\]

\[c_{5} = \frac{1 - ( - 1)^{5}}{2 \cdot 5 + 1} = \frac{2}{11}.\]

\[\boxed{\text{670.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[Пусть\ существуют\ числа\ \]

\[a_{1},a_{2},a_{3},\ которые\ являются\ \]

\[членами\ и\ арифметической,\ \]

\[и\ геометрической\ прогрессий.\ \]

\[Тогда:\]

\[a_{2} = a_{1} + d = a_{1} \cdot q;\]

\[a_{3} = a_{1} + 2d = a_{1} \cdot q^{2}.\]

\[\left\{ \begin{matrix} d = a_{1} \cdot q - a_{1}\text{\ \ \ } \\ 2d = a_{1} \cdot q^{2} - a_{1} \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} d = a_{1}q - a_{1}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ 2a_{1} \cdot q - 2a_{1} = a_{1} \cdot q^{2} - a_{1} \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} d = a_{1}q - a_{1}\text{\ \ \ \ } \\ q^{2} - 1 = 2q - 2 \\ \end{matrix} \Longrightarrow \right.\ \]

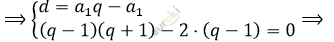
\[\Longrightarrow \left\{ \begin{matrix} d = a_{1}q - a_{1}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ (q - 1)(q + 1 - 2) = 0 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} d = a_{1}q - a_{1}\ \\ q - 1 = 0\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} q = 1 \\ d = 0 \\ \end{matrix} \right.\ \]

\[\Longrightarrow a_{1} = a_{2} = a_{3} \Longrightarrow\]

\[\Longrightarrow нет\ таких\ чисел.\]