Решебник по алгебре 9 класс Макарычев Задание 610

 

\[\boxed{\text{610}\text{\ \ (610)}\text{.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[x_{1} = 10,\ \ d = 3:\ \ \]

\[x_{15} = x_{1} + d \cdot (15 - 1) = 10 + 3 \cdot 14 = 52;\]

\[x_{30} = 10 + 3 \cdot (30 - 1) = 97;\ \ \ \]

\[S_{n} = \frac{(x_{1} + x_{n})}{2} \cdot n;\]

\[S_{16} = \frac{x_{15} + x_{30}}{2} \cdot 16 = (52 + 97) \cdot 8 = 1192.\]

\[\boxed{\text{610.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[x_{1} = a,\ \ x_{2} = a + d,\ \ \]

\[x_{3} = a + 2d,\ \ \]

\[x_{2} - 1 = aq,\ \ x_{3} + 1 = aq^{2},\]

\[\left\{ \begin{matrix} a + d = aq + 1\ \ \ \\ a + 2d = aq^{2} - 1 \\ \end{matrix} \Longrightarrow \right.\ \]

\[\Longrightarrow \left\{ \begin{matrix} a(q - 1) = d - 1\ \ \ \ \\ a\left( q^{2} - 1 \right) = 2d + 1 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} \frac{a(q + 1)(q - 1)}{a(q - 1)} = \frac{2d + 1}{d - 1} \\ d - 1 = a(q - 1)\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} q = \frac{d + 2}{d - 1} \\ a = \frac{d - 1}{q - 1} \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} q = \frac{d + 2}{d - 1}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ a = \frac{d - 1}{\frac{d + 2 - d + 1}{d - 1}} \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} q = \frac{d + 2}{d - 1}\text{\ \ \ \ } \\ a = \frac{(d - 1)²}{3} \\ \end{matrix} \right.\ \]

\[a + a + d + 2d = 21\]

\[3a + 3d = 21\]

\[a + d = 7\]

\[\frac{(d - 1)^{2}}{3} + d = 7\]

\[d^{2} - 2d + 1 + 3d = 21\]

\[d^{2} + d - 20 = 0\]

\[D = 1 + 80 = 81\]

\[d = \frac{- 1 \pm 9}{2},\ \ d_{1} = - 5,\ \ \]

\[d_{2} = 4,\]

\[1)\ \left\{ \begin{matrix} d = - 5\ \ \ \ \\ a + d = 7 \\ \end{matrix} \right.\ \Longrightarrow\]

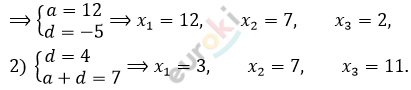
\[Ответ:3,\ 7,\ 11\ или\ 12,\ 7,\ 2.\]