Решебник по алгебре 9 класс Макарычев Задание 544

\[\boxed{\text{544\ (544).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ длины\ сторон\ \]

\[прямоугольника\ \text{x\ }и\ y\text{.\ }\]

\[По\ теореме\ Пифагора:\]

\[x^{2} + y^{2} = 15^{2}\text{.\ }\]

\[Составим\ систему\ уравнений:\]

\[\Longrightarrow \left\{ \begin{matrix} x^{2} + y^{2} = 225\ \ \ \ \ \ \ \ \\ x + y - 14 = \frac{x + y}{3} \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x^{2} + y^{2} = 225 \\ x + y = 21\ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} y = 21 - x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 2x^{2} - 42x + 216 = 0 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} y = 21 - x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} - 21x + 108 = 0 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x_{1} = 9\ \ \\ y_{1} = 12 \\ \end{matrix} \right.\ \ \ \ \ или\ \ \ \left\{ \begin{matrix} x_{2} = 12 \\ y_{2} = 9\ \ . \\ \end{matrix} \right.\ \]

\[Ответ:9\ см\ и\ 12\ см.\]

\[\boxed{\text{544.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

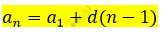
\[\textbf{а)}\ a_{1} = - 3;\ \ d = 0,7:\]

\[a_{n} = - 3 + 0,7 \cdot (n - 1)\]

\[a_{11} = - 3 + 0,7 \cdot 10 = 4.\]

\[\textbf{б)}\ a_{1} = 18;\ \ d = - 0,6:\ \]

\[a_{n} = 18 - 0,6 \cdot (n - 1)\]

\[a_{26} = 18 - 0,6 \cdot 25 = 3.\]