Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Макарычев Задание 510
Задание 510
\[\boxed{\text{510\ (510).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\textbf{а)}\ \left\{ \begin{matrix} x^{2} + 3xy - 10y^{2} = 0 \\ x^{2} - 4xy + 3y = 0\ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} (x + 5y)(x - 2y) = 0 \\ x² - 4xy + 3y = 0\ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[1)\ \left\{ \begin{matrix} x + 5y = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} - 4xy + 3y = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = - 5y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 25y^{2} + 20y^{2} + 3y = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = - 5y\ \ \ \ \ \ \ \ \ \ \\ 45y^{2} + 3y = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = - 5y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 3y(15y + 1) = 0 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} y_{1} = 0 \\ x_{1} = 0 \\ \end{matrix} \right.\ \ \]
\[\ или\left\{ \begin{matrix} y_{2} = - \frac{1}{15} \\ x_{2} = \frac{1}{3}\text{.\ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[2)\ \left\{ \begin{matrix} x - 2y = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} - 4xy + 3y = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = 2y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 4y^{2} - 8y^{2} + 3y = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = 2y\ \ \ \ \ \ \ \ \ \ \ \ \ \\ y(3 - 4y) = 0 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} y_{1} = 0 \\ x_{1} = 0 \\ \end{matrix} \right.\ \text{\ \ \ }\]
\[или\ \left\{ \begin{matrix} y_{2} = 0,75 \\ x_{2} = 1,5.\ \ \\ \end{matrix} \right.\ \]
\[\textbf{б)}\ \left\{ \begin{matrix} x^{2} + xy - 6y^{2} = 0\ \ \ \ \ \ \ \\ x^{2} + 3xy + 2y - 6 = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} (x + 3y)(x - 2y) = 0\ \ \\ x² + 3xy + 2y - 6 = 0 \\ \end{matrix} \right.\ \]
\[1)\ \left\{ \begin{matrix} x + 3y = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 3xy + 2y - 6 = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = - 3y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 9y^{2} - 9y^{2} + 2y - 6 = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \ \left\{ \begin{matrix} x = - 3y \\ 2y = 6\ \ \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} y = 3\ \ \\ x = - 9 \\ \end{matrix} \right.\ ;\]
\[2)\ \left\{ \begin{matrix} x - 2y = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 3xy + 2y - 6 = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = 2y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 4y^{2} + 6y^{2} + 2y - 6 = 0 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = 2y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 5y² + y - 3 = 0 \\ \end{matrix} \right.\ \]
\[5y^{2} + y - 3 = 0\]
\[D = 1 + 4 \cdot 5 \cdot 3 = 61\]
\[y_{1,2} = \frac{- 1 \pm \sqrt{61}}{10};\ \]
\[\Longrightarrow \left\{ \begin{matrix} y_{1} = \frac{- 1 + \sqrt{61}}{5} \\ x_{1} = \frac{- 1 + \sqrt{61}}{10} \\ \end{matrix} \right.\ \text{\ \ \ \ }\]
\[или\left\{ \begin{matrix} y_{2} = \frac{- 1 - \sqrt{61}}{5} \\ x_{2} = \frac{- 1 - \sqrt{61}}{10}. \\ \end{matrix} \right.\ \]
\[Ответ:а)\ (0;0);(1,5;0,75);\]
\[\left( \frac{1}{3};\ - \frac{1}{15} \right);\]
\[\textbf{б)}\ ( - 9;3);\]
\[\left( \frac{- 1 + \sqrt{61}}{5};\frac{- 1 + \sqrt{61}}{10} \right);\]
\[\left( \frac{- 1 - \sqrt{61}}{5};\frac{- 1 - \sqrt{61}}{10} \right)\text{.\ }\]
\[\boxed{\text{510.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]
\[Пусть\ первая\ труба\ заполняет\ \]
\[бассейн\ за\ \text{x\ }ч,\ а\ вторая -\]
\[за\ \text{y\ }ч.\]
\[Тогда\ за\ час\ первая\ труба\ \]
\[наполнит\ \ \frac{1}{x}\ часть\ бассейна,\ а\ \]
\[вторая - \frac{1}{y}.\]
\[Составим\ систему\ уравнений:\]
\[\left\{ \begin{matrix} y = x + 5\ \ \ \\ \frac{5}{x} + \frac{7,5}{y} = 1 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} y = x + 5\ \ \ \ \ \ \ \ \ \ \\ 5y + 7,5x = xy \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} y = x + 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 10y + 15x = 2xy \\ \end{matrix} \right.\ \Longrightarrow\]
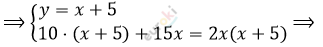
\[\Longrightarrow \left\{ \begin{matrix} y = x + 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 2x² - 15x - 50 = 0 \\ \end{matrix} \right.\ \]
\[D = 15^{2} + 2 \cdot 50 \cdot 4 = 625\]
\[x_{1,2} = 10;\ - \frac{5}{2};\ \]
\[1)\ x_{1} = - \frac{5}{2} \Longrightarrow\]
\[\Longrightarrow не\ подходит\ по\ условию;\]
\[2)\ x_{2} = 10,\ \ \]
\[y_{2} = 15 \Longrightarrow \frac{1}{x} + \frac{1}{y} = \frac{1}{10} + \frac{1}{15} =\]
\[= \frac{1}{6} \Longrightarrow за\ 6\ часов.\]
\[Ответ:бассейн\ наполнится\ \]
\[за\ 6\ часов\ совместной\ работы.\]
