Решебник по алгебре 9 класс Макарычев Задание 465

 

\[\boxed{\text{465\ (465).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ катеты\ треугольника\]

\[\ равны\ x\ и\ y\ см.\ \]

\[По\ теореме\ Пифагора:\]

\[x^{2} + y^{2} = 13^{2}.\]

\[Если\ один\ и\ катетов\ равен\ \]

\[(x + 4)\ см,\ то\ гипотенуза\ \]

\[станет\ равна:\]

\[(x + 4)^{2} + y^{2} = (13 + 2)^{2}.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} x^{2} + y^{2} = 169\ \ \ \ \ \ \ \ \ \ \ \\ (x + 4)^{2} + y^{2} = 225 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} y^{2} = 169 - x^{2}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ x^{2} + 8x + 16 + 169 - x^{2} = 225 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\left\{ \begin{matrix} y^{2} = 169 - x^{2} \\ 8x = 40\ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} x = 5\ \ \ \ \ \ \ \\ y^{2} = 144 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x = 5\ \ \ \\ y = 12 \\ \end{matrix}. \right.\ \]

\[Ответ:5\ см\ и\ 12\ см.\]

\(\boxed{\text{465.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\)

\[\textbf{а)}\ \left\{ \begin{matrix} y \geq x² \\ y \leq 4\ \ \\ \end{matrix} \right.\ \]

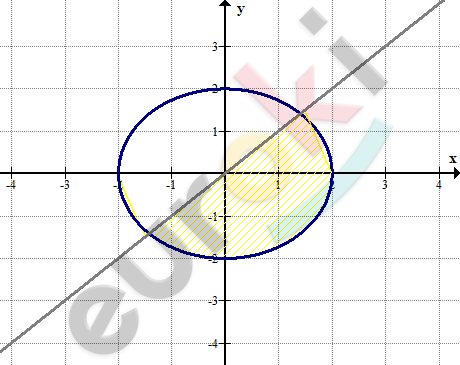
\[\textbf{б)}\ \left\{ \begin{matrix} x^{2} + y^{2} \leq 4 \\ x - y \geq 0\ \ \ \ \ \\ \end{matrix} \right.\ \]

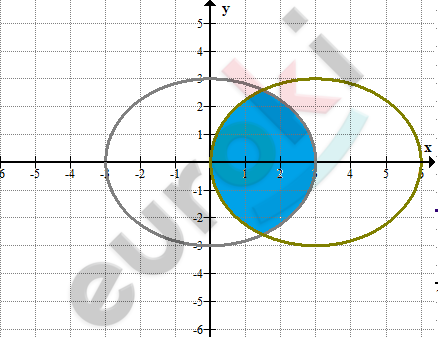
\[\textbf{в)}\ \left\{ \begin{matrix} x^{2} + y^{2} \leq 9\ \ \ \ \ \ \ \ \ \ \ \\ (x - 3)^{2} + y^{2} \leq 9 \\ \end{matrix} \right.\ \]

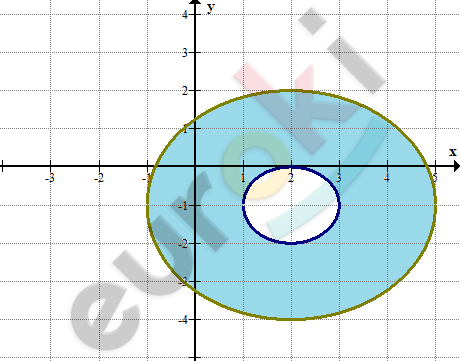
\[\textbf{г)}\ \left\{ \begin{matrix} (x - 2)^{2} + (y + 1)^{2} \geq 1 \\ (x - 2)^{2} + (y + 1)^{2} \leq 9 \\ \end{matrix} \right.\ \ \]