Решебник по алгебре 9 класс Макарычев Задание 406

 

\[\boxed{\text{406\ (406).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[x^{2} + y^{2} - 6 \cdot (x - y) = 7\]

\[x^{2} + y^{2} - 6x + 6y = 7\]

\[\left( x^{2} - 6x + 9 \right) +\]

\[+ \left( y^{2} + 6y + 9 \right) = 25\]

\[(x - 3)^{2} + (y + 3)^{2} = 25\]

\[Получили\ уравнение\ \]

\[окружности\ с\ центром\ \]

\[в\ точке\ (3; - 3)\ и\]

\[радиусом\ r = 5.\]

\[Значит,\ график\ уравнения\ \]

\[x^{2} + y^{2} - 6 \cdot (x - y) =\]

\[= 7 - окружность.\]

\[Что\ и\ требовалось\ доказать.\]

\(\boxed{\text{406.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\)

\[x^{2} + y^{2} = 9;\ \ \ y = c\]

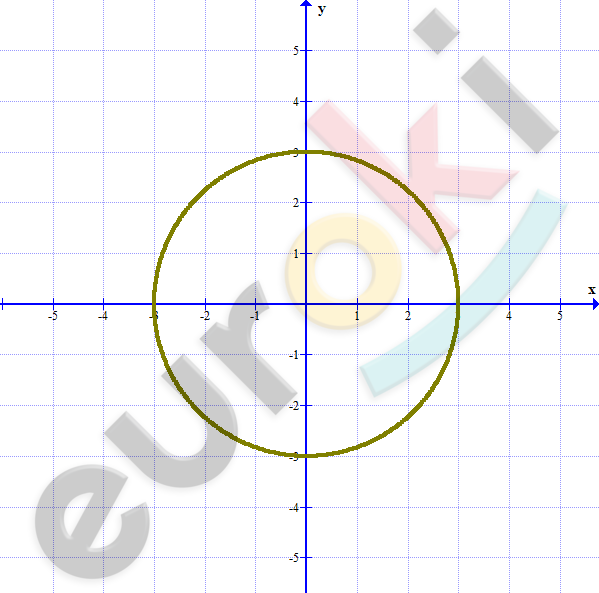
\[\textbf{а)}\ пересекаются:\]

\[при\ \ - 3 < c < 3.\]

\[\textbf{б)}\ не\ имеют\ общих\ точек:\]

\[при\ c < - 3;\ \ c > 3.\]

\[\textbf{в)}\ касается\ (одна\ точка):\]

\[при\ c = \pm 3.\]