Решебник по алгебре 9 класс Макарычев Задание 405

 

\[\boxed{\text{405\ (405).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\text{K\ }(2;\ - 5):\]

\[(x - 2)^{2} + (y + 5)^{2} = r^{2}.\]

\[\textbf{а)}\ A\ ( - 1; - 1):\]

\[( - 1 - 2)^{2} + ( - 1 + 5)^{2} =\]

\[= 9 + 16 = 25\]

\[(x - 2)^{2} + (y + 5)^{2} = 25.\]

\[\textbf{б)}\ B\ ( - 3;7):\]

\[( - 3 - 2)^{2} + (7 + 5)^{2} =\]

\[= 25 + 141 = 169\]

\[(x - 2)^{2} + (y + 5)^{2} = 169.\]

\[\textbf{в)}\ C\ (1;\ - 4):\]

\[(1 - 2)^{2} + ( - 4 + 5)^{2} =\]

\[= 1 + 1 = 2\]

\[(x - 2)^{2} + (y + 5)^{2} = 2.\]

\[\textbf{а)}\ \left\{ \begin{matrix} x^{2} + y^{2} = 9 \\ y = 2x + 3\ \ \\ \end{matrix} \right.\ \]

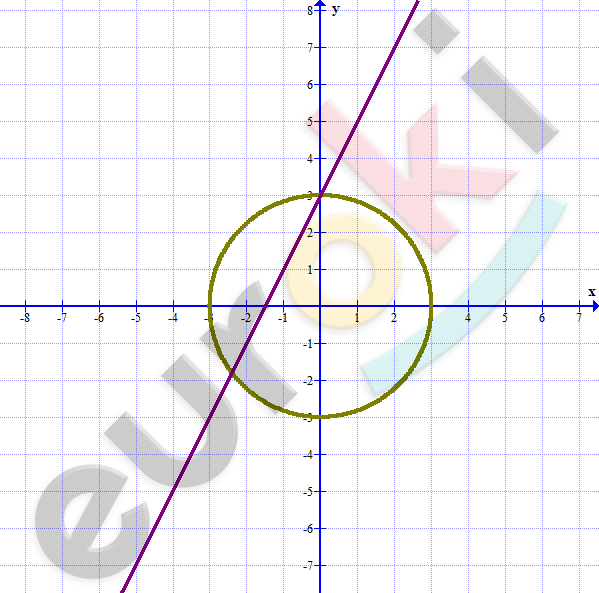
\[Две\ точки\ пересечения.\]

\[\textbf{б)}\ \left\{ \begin{matrix} x^{2} + y^{2} = 7 \\ y - 4x = 2\ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\left\{ \begin{matrix} x^{2} + y^{2} = 7 \\ y = 4x + 2\ \ \\ \end{matrix} \right.\ \]

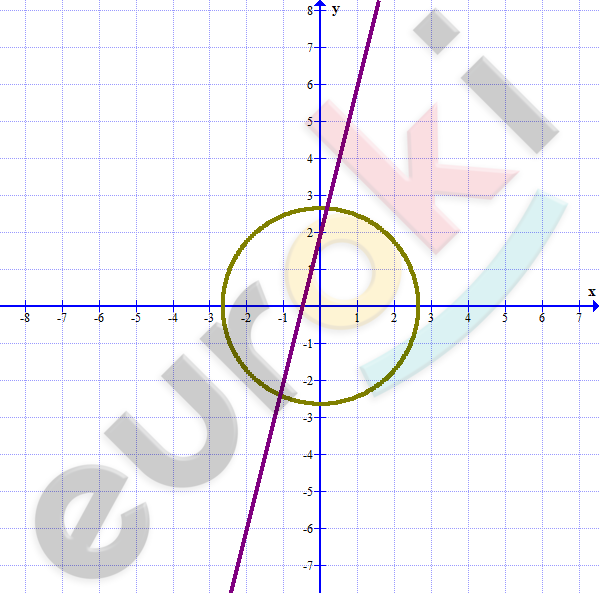
\[Две\ точки\ пересечения.\]

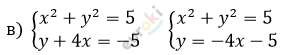
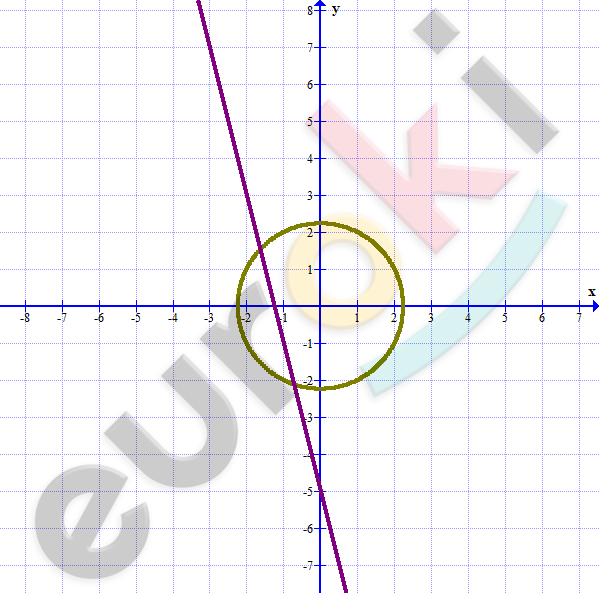
\[Две\ точки\ пересечения.\]