Решебник по алгебре 9 класс Макарычев Задание 374

 

\[\boxed{\text{374\ (374).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[3\frac{1}{4} \cdot \left( a + \frac{1}{a} \right) = a^{3} + \frac{1}{a^{3}}\]

\[\frac{13}{4} \cdot \left( a + \frac{1}{a} \right) = a^{3} + \frac{1}{a^{3}}\]

\[Пусть\ \ y = a + \frac{1}{a};\ \ \ \ \]

\[y^{3} = \left( a + \frac{1}{a} \right)^{3} =\]

\[= a^{3} + \frac{1}{a^{3}} + \frac{3}{a} + 3a;\]

\[a^{3} + \frac{1}{a^{3}} = y^{3} - 3 \cdot \left( a + \frac{1}{a} \right) =\]

\[= y^{3} - 3y:\ \]

\[\frac{13}{4}y = y^{3} - 3y\]

\[4y^{3} - 12y - 13y = 0\ \]

\[4y^{3} - 25y = 0\]

\[y \cdot \left( 4y^{2} - 25 \right) = 0\]

\[y(2y - 5)(2y + 5) = 0\]

\[4y(y - 2,5)(y + 2,5) = 0\]

\[y_{1} = 0;\ \ y_{2} = 2,5;\ \ y_{3} = - 2,5.\]

\[1)\ a + \frac{1}{a} = 0\]

\[a^{2} + 1 = 0 \Longrightarrow корней\ нет.\]

\[2)\ a + \frac{1}{a} = 2,5\]

\[a^{2} - 2,5a + 1 = 0\ \ \]

\[2a^{2} - 5a + 2 = 0\]

\[D = 25 - 4 \cdot 2 \cdot 2 = 9\]

\[a_{1,2} = \frac{5 \pm 3}{4} = 2;\frac{1}{2}\text{.\ }\]

\[3)\ a + \frac{1}{a} = - 2,5\]

\[\left( a + \frac{1}{a} \right)\ в\ 3\frac{1}{4}\ больше \Longrightarrow\]

\[\Longrightarrow не\ подходят.\]

\[Ответ:a = \frac{1}{2};\ \ a = 2.\]

\[\boxed{\text{374.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

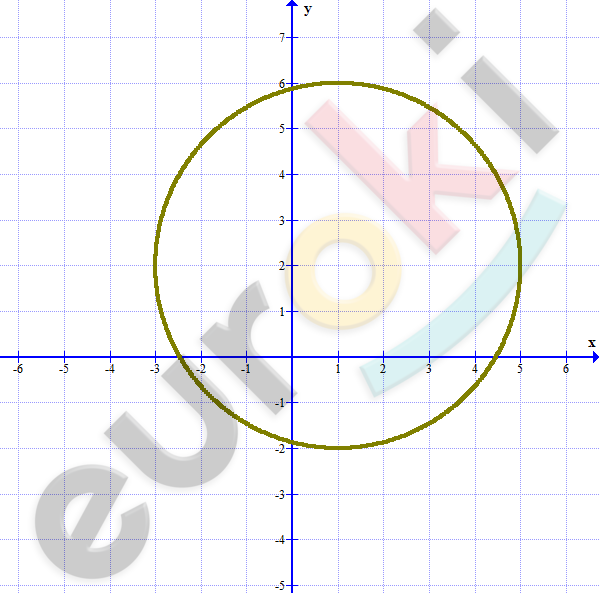
\[\textbf{а)}\ (x - 1)^{2} + (y - 2)^{2} = 16\]

\[окружность\ с\ центром\ (1;2)\ и\ \]

\[R = 4.\]

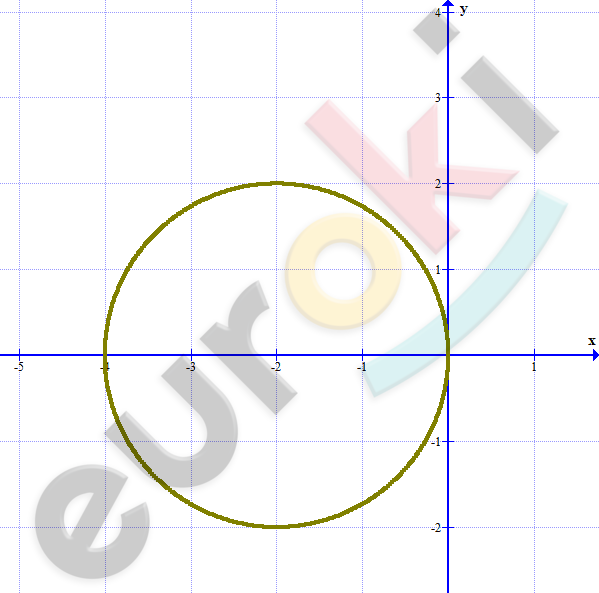
\[\textbf{б)}\ (x + 2)^{2} + y^{2} = 4.\ \]

\[окружность\ с\ центром\ \]

\[( - 2;0)\ и\ R = 2.\]

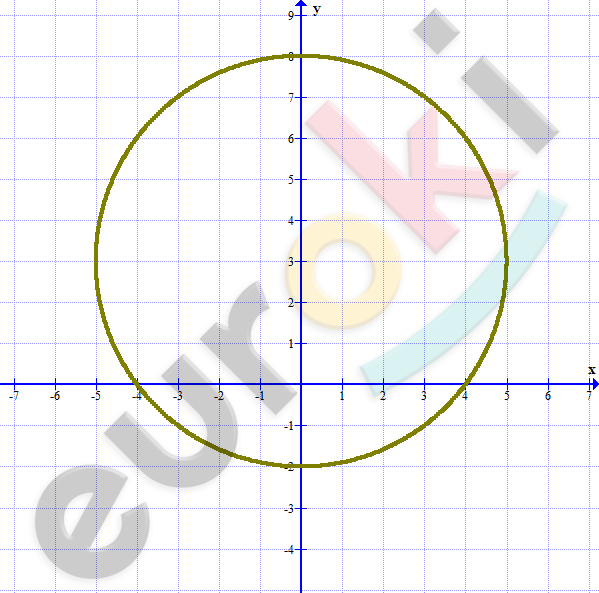
\[\textbf{в)}\ x^{2} + (y - 3)^{2} = 25\]

\[окружность\ с\ центром\ (0;3)\ и\ \]

\[R = 5.\]

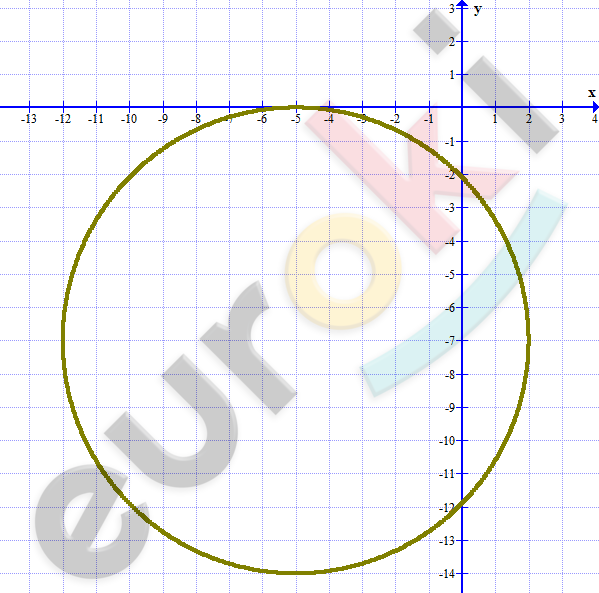
\[\textbf{г)}\ (x + 5)^{2} + (y + 7)^{2} = 49\]

\[окружность\ с\ центром\ \]

\[( - 5; - 7)\ и\ R = 7.\]