Решебник по алгебре 9 класс Макарычев Задание 319

 

\[\boxed{\text{319\ (319).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ \ x - ширина\ \]

\[прямоугольника,\ \]

\[(x + 5) - его\ длина.\]

\[Площадь\ S = x(x + 5);\ \ \]

\[S > 36 - по\ условию.\]

\[Составим\ неравенство:\]

\[x(x + 5) > 36\]

\[x^{2} + 5x - 36 > 0\]

\[x_{1} + x_{2} = - 5;\ \ \ x_{1} \cdot x_{2} = - 36\]

\[x_{1} = 4;\ \ x_{2} = - 9;\]

\[(x + 9)(x - 4) > 0\]

\[x \in ( - \infty;9) \cup (4;\ + \infty).\]

\[Но\ так\ как\ x - сторона\ \]

\[прямоугольника,\ то\ x > 0 \Longrightarrow\]

\[\Longrightarrow x \in (4; + \infty).\]

\[Ответ:больше\ 4\ см.\]

\[\boxed{\text{319.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[x^{3} = x\]

\[1)\ y = x\]

\[y = x^{3}\]

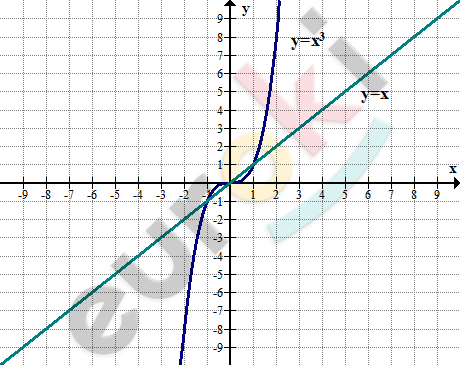
\[Исходя\ из\ графика:\]

\[x_{1} = 0,\ \ x_{2} = 0,\ \ \]

\[x_{3} = - 1.\]

\[2)\ Аналитически:\]

\[x^{3} = x\]

\[x^{3} - x = 0\]

\[x\left( x^{2} - 1 \right) = 0\]

\[x(x - 1)(x + 1) = 0\]

\[x_{1} = 0,\ \ x_{2} = 1,\ \ \]

\[x_{3} = - 1.\]

\[Ответ:\ - 1;0;1.\]