Решебник по алгебре 9 класс Макарычев Задание 199

\[\boxed{\text{199}\text{\ (199)}\text{.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\frac{(a + b)^{\frac{1}{2}} + (a - b)^{\frac{1}{2}}}{(a + b)^{\frac{1}{2}} - (a - b)^{\frac{1}{2}}} = 2\]

\[Упростим\ левую\ часть:\]

\[\frac{(a + b)^{\frac{1}{2}} + (a - b)^{\frac{1}{2}}}{(a + b)^{\frac{1}{2}} - (a - b)^{\frac{1}{2}}} =\]

\[= \frac{\sqrt{a + b} + \sqrt{a - b}}{\sqrt{a + b} - \sqrt{a - b}} =\]

\[= \frac{a + b + a - b + 2\sqrt{a^{2} - b^{2}}}{a + b - a + b} =\]

\[= \frac{2a + 2\sqrt{a^{2} - b^{2}}}{2b} =\]

\[= \frac{a + \sqrt{a^{2} - b^{2}}}{b};\]

\[при\ \ b = \frac{4a}{5}:\ \ \ \]

\[\frac{a + \sqrt{a^{2} - b^{2}}}{b} =\]

\[= \frac{a + \sqrt{a^{2} - \frac{16a^{2}}{25}}}{\frac{4a}{5}} =\]

\[= \frac{a + a\sqrt{\frac{25 - 16}{25}}}{\frac{4a}{5}} = \frac{1 + \sqrt{\frac{9}{25}}}{\frac{4}{5}} =\]

\[= \left( 1 + \frac{3}{5} \right)\ :\frac{4}{5} = \frac{8}{5} \cdot \frac{5}{4} = 2.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{199}\text{.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

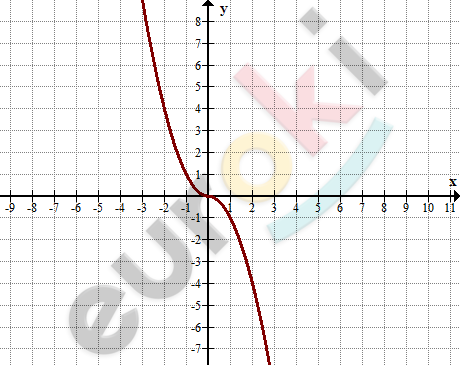
\[\textbf{а)}\ y = x|x|\]

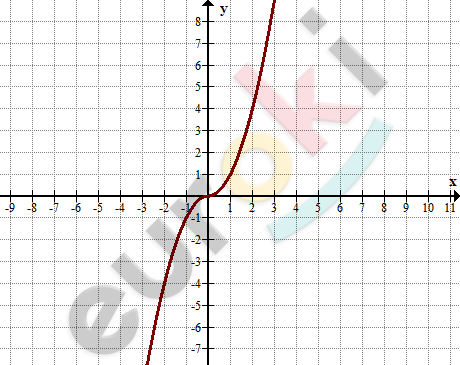
\[\textbf{б)}\ y = - \frac{x^{3}}{|x|}\]