Решебник по алгебре 9 класс Макарычев Задание 171

 

\[\boxed{\text{171\ (}\text{н}\text{).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\mathbf{Если\ }\mathbf{a > 0;\ \ n -}\mathbf{натуральное\ }\]

\[\mathbf{число,\ больше\ 1,\ то:}\]

\[\sqrt[\mathbf{n}]{\mathbf{a}}\mathbf{=}\mathbf{a}^{\frac{\mathbf{1}}{\mathbf{n}}}\mathbf{.}\]

Решение.

\[\textbf{а)}\ \left( \sqrt{10} \right)^{2} = \left( 10^{\frac{1}{2}} \right)^{2} = 10\]

\[\textbf{б)}\ \left( \sqrt[3]{5} \right)^{3} = \left( 5^{\frac{1}{3}} \right)^{3} = 5\]

\[\textbf{в)}\ \left( - \sqrt[4]{12} \right)^{4} = \left( - 12^{\frac{1}{4}} \right)^{4} = 12\]

\[\textbf{г)}\ \left( 2\sqrt[5]{- 2} \right)^{5} = 2^{5} \cdot \left( - 2^{\frac{1}{5}} \right)^{5} =\]

\[= 2^{5} \cdot ( - 2)^{1} = - 2^{6} = - 64\ \]

\[\textbf{д)}\ \left( \sqrt[5]{- 8} \right)^{5} = \left( - 8^{\frac{1}{5}} \right)^{5} =\]

\[= ( - 8)^{1} = - 8\]

\[\textbf{е)}\ \left( - 2\sqrt{3} \right)^{2} = 4\left( \sqrt{3} \right)^{2} =\]

\[= 4 \cdot 3 = 12\]

\[\boxed{\text{171\ (}\text{с}\text{).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\mathbf{Если\ }\mathbf{a > 0;\ \ n -}\mathbf{натуральное\ }\]

\[\mathbf{число,\ больше\ 1,\ то:}\]

\[\sqrt[\mathbf{n}]{\mathbf{a}}\mathbf{=}\mathbf{a}^{\frac{\mathbf{1}}{\mathbf{n}}}\mathbf{.}\]

Решение.

\[\textbf{а)}\ \left( \sqrt{10} \right)^{2} = \left( 10^{\frac{1}{2}} \right)^{2} = 10\]

\[\textbf{б)}\ \left( \sqrt[3]{5} \right)^{3} = \left( 5^{\frac{1}{3}} \right)^{3} = 5\]

\[\textbf{в)}\ \left( - \sqrt[4]{12} \right)^{4} = \left( - 12^{\frac{1}{4}} \right)^{4} = 12\]

\[\textbf{г)}\ \left( 2\sqrt[5]{- 2} \right)^{5} = 2^{5} \cdot \left( - 2^{\frac{1}{5}} \right)^{5} =\]

\[= 2^{5} \cdot ( - 2)^{1} = - 2^{6} = - 64\ \]

\[\boxed{\text{171.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

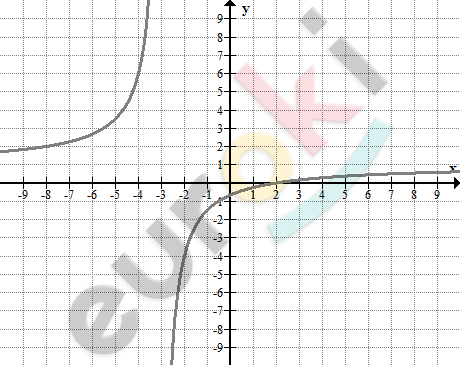
\[y = \frac{k}{x - m} + n,\ \ где\ k < 0:\]

\[\textbf{а)}\ m > 0,\ \ n < 0;\]

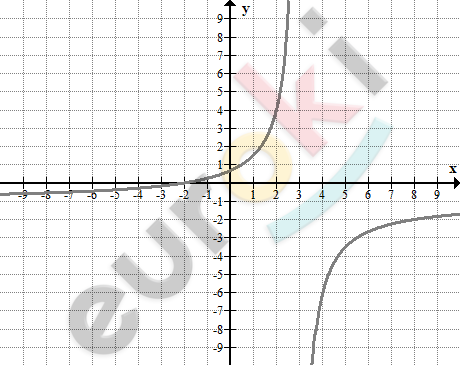
\[\textbf{б)}\ \ m < 0,\ \ n > 0\]