Решебник по алгебре 9 класс Макарычев Задание 10

 

\[\boxed{\text{10\ (10).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ Подойдет\ линейная\ или\ \]

\[квадратичная\ функция:\]

\[f(x) = x^{2} + 8;\]

\[f(x) = 7x + 2.\]

\[\textbf{б)}\ Подойдет\ любая\ \]

\[дробно - рациональная\ \]

\[функция,\ знаменатель\]

\[которой\ обращается\ в\ ноль\ \]

\[при\ x = 7:\]

\[f(x) = \frac{1}{2x - 14}.\]

\[\boxed{\text{10.\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[Докажем,\ что\ разность\ двух\ \]

\[рациональных\ чисел\ есть\ \]

\[число\ рациональное.\ \]

\[Возьмем\ \frac{p}{q}\ и\ \frac{r}{s} -\]

\[2\ рациональных\ числа:\]

\[p \cdot q \cdot r \cdot s - целые.\]

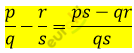
\[Числа\ ps - qr,\ qs - целые,\ \]

\[так\ как\ целые\ числа\ замкнуты\]

\[относительно\ операций\ \]

\[умножения\ и\ вычитания.\ \]

\[Следовательно:\]

\[Произведение.\]

\[Пусть\ \frac{p}{q}\ и\ \frac{r}{s} -\]

\[два\ рациональных\ числа;\]

\[p,\ q,\ r,\ s - целые.\]

\[\frac{p}{q} \cdot \frac{r}{s} = \frac{\text{pr}}{\text{qs}},\ где\ \text{pr\ }и\ qs -\]

\[целые\ числа.\]

\[Следовательно:\]

\[Частное.\]

\[Пусть\ \frac{p}{q}\ и\ \frac{r}{s} -\]

\[рациональные\ числа;\ \ \ \]

\[\ p,\ q,\ r,\ s - целые.\]

\[\frac{p}{q}\ :\frac{r}{s} = \frac{\text{ps}}{\text{qr}},\ где\ \text{ps\ }и\ \ \]

\[qr - целые\ числа.\]

\[Следовательно:\ \ \]