Решебник по алгебре 9 класс Мерзляк Задание 848

 

\[\boxed{\mathbf{848\ (848).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Запишем\ прогрессию:\ \]

\[\ b_{1},b_{2},b_{3},\ldots,\ b_{k},\ b_{n - k + 1},\ldots,\ b_{n}.\]

\[Получаем:\]

\[{b_{n} = b_{1} \cdot q^{n - 1}\text{\ \ } }{b_{k} = b_{1} \cdot q^{k - 1}\text{\ \ }}\]

\[b_{n - k + 1} = b_{1}q^{n - k + 1 - 1} = b_{1}q^{n - k}\]

\[b_{1}b_{n} = b_{1} \cdot b_{1}q^{n - 1} = b_{1}^{2} \cdot q^{n - 1}\]

\[b_{k} \cdot b_{n - k + 1} = b_{1}q^{k - 1} \cdot b_{1}q^{n - k} =\]

\[= b_{1}^{2} \cdot q^{k - 1 + n - k} = b_{1}^{2} \cdot q^{n - 1}.\]

\[Отсюда:\ \ \ \]

\[b_{1}b_{n} = \ b_{k} \cdot b_{n - k + 1}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{848.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ числа\ a_{1},\ a_{2},\ a_{3},\]

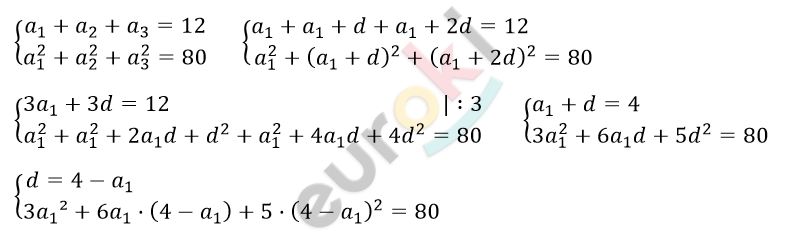
\[3a_{1}^{2} + 24a_{1} - 6a_{1}^{2} +\]

\[+ 5 \cdot \left( 16 - 8a_{1} + a_{1}^{2} \right) = 80\]

\[3a_{1}^{2} + 24a_{1} - 6a_{1}^{2} + 80 -\]

\[- 40a_{1} + 5a_{1}^{2} = 80\]

\[2a_{1}^{2} - 16a_{1} = 0,\ \ \]

\[2a_{1}\left( a_{1} - 8 \right) = 0,\ \ \]

\[a_{1} = 0\ \ или\ \ \ a_{1} = 8\]

\[a_{1} = 0,\ \ a_{2} = a_{1} + d,\ d = 4 -\]

\[- a_{1} = 4,\ \ a_{2} = 0 + 4 = 4,\ \ \]

\[a_{3} = 4 + 4 = 8\]

\[a_{1} = 8,\ \ d = 4 - 8 = - 4,\]

\[\text{\ \ }a_{2} = 8 - 4 = 4,\ \ \]

\[a_{3} = 4 - 4 = 0\]

\[Ответ:0;4;8.\]