Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Мерзляк Задание 797
Задание 797
\[\boxed{\mathbf{797\ (797).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]
\[1;3;5;7;\ldots\ \ \]
\[d = 3 - 1 = 2\]
\[S_{n} = \frac{2a_{1} + d(n - 1)}{2} \cdot n =\]
\[= \frac{2 \cdot 1 + 2 \cdot (n - 1)}{2} \cdot n =\]
\[= \frac{2 + 2n - 2}{2} \cdot n = n^{2}\]
\[400 < S_{n} < 500\]
\[400 < n^{2} < 500\]
\[\sqrt{400} < n < \sqrt{500}\]
\[20 < n < 22,3,\]
\[\text{\ \ }тогда\ n = 21\]
\[21 - нечетных\ страницы;\]
\[21 \cdot 2 = 42\ (страницы) - всего\ \]
\[в\ книге.\]
\[Ответ:42\ страницы.\]
\[\boxed{\mathbf{797.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]
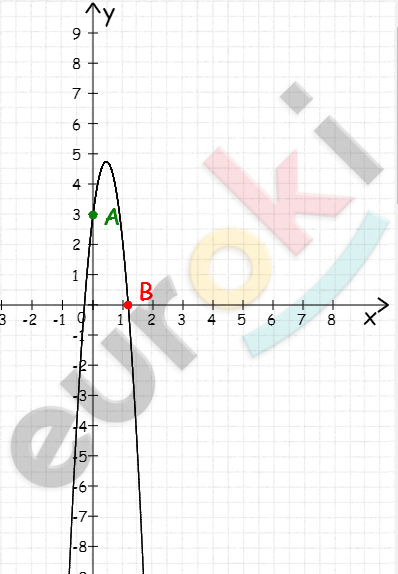
\[1)\ y = - 2x^{2} + 1\]
\[x_{0} = 0,\ \ y_{0} = 1\]
\[ветви\ вниз;\]
\[E(y) = ( - \infty;1\rbrack\]
\[Возрастает\ ( - \infty;0\rbrack;\]
\[убывает\ \lbrack 0; + \infty).\]
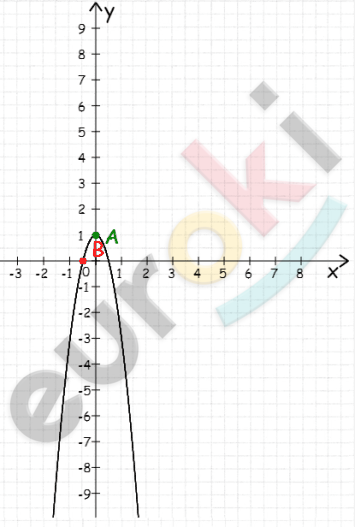
\[2)\ y = 0,5x² - 2\]
\[x_{0} = 0,\ \ y_{0} = - 2\]
\[ветви\ вверх;\]
\[E(y) = \lbrack - 2; + \infty)\]
\[убывает\ ( - \infty;0\rbrack;\]
\[возрастает\ \lbrack 0; + \infty).\]
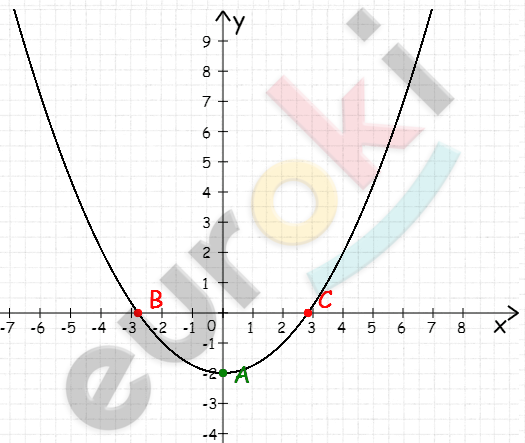
\[3)\ y = x² + 6x + 5\]
\[x_{0} = - \frac{6}{2} = - 3,\ \ \]
\[y_{0} = 9 - 18 + 5 = - 4\]
\[ветви\ вверх;\]
\[E(y) = \lbrack - 4; + \infty)\]
\[Убывает\ ( - \infty; - 3\rbrack;\]
\[возрастает\ \ \lbrack - 3; + \infty).\]
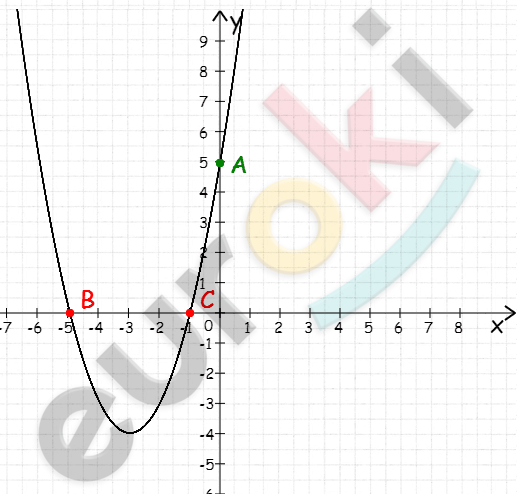
\[4)\ y = 4x - x²\]
\[x_{0} = \frac{- 4}{- 2} = 2,\ \ y_{0} = 8 - 4 = 4\]
\[ветви\ вниз;\]
\[E(y) = ( - \infty;4\rbrack\]
\[Возрастает\ ( - \infty;2\rbrack;\]
\[убывает\ \lbrack 2; + \infty).\]
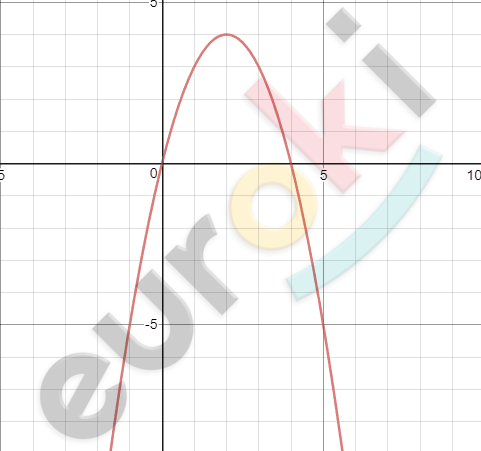
\[5)y = - x^{2} + 4x - 3\]
\[x_{0} = \frac{- 4}{- 2} = 2,\ \ \]
\[y_{0} = - 4 + 8 - 3 = 1\]
\[ветви\ вниз;\]
\[E(y) = ( - \infty;1\rbrack\]
\[Возрастает\ ( - \infty;2\rbrack;\]
\[убывает\ \lbrack 2; + \infty).\]
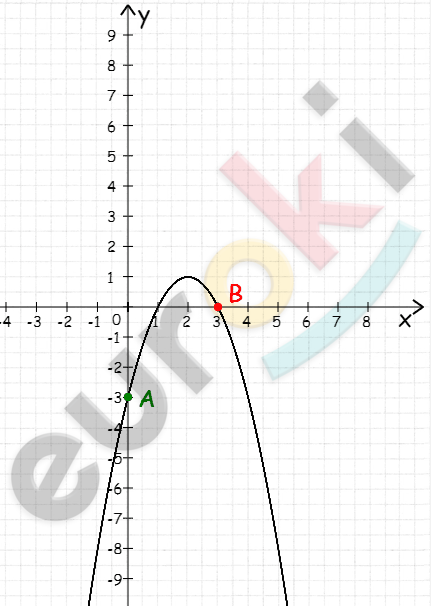
\[6)\ y = x² - 4x + 5\]
\[x_{0} = \frac{4}{2} = 2,\ \ \]
\[y_{0} = 4 - 8 + 5 = 1\]
\[ветви\ вверх;\]
\[E(y) = \lbrack 1; + \infty)\]
\[Убывает\ ( - \infty; - 2\rbrack;\]
\[возрастает\ \ \lbrack 2; + \infty).\]
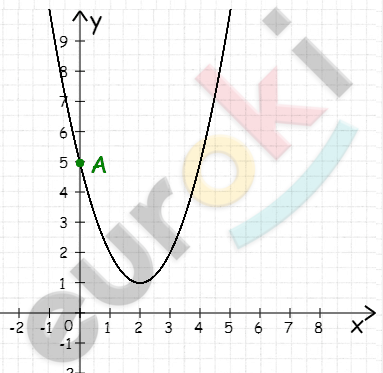
\[7)\ y = 2x² - 3x - 2\]
\[x_{0} = \frac{3}{4},\ \ \]
\[y_{0} = \frac{2 \cdot 9}{16} - \frac{9}{4} - 2 =\]
\[= \frac{18 - 36 - 32}{16} = - 3\frac{1}{8}\]
\[ветви\ вверх;\]
\[E(y) = \lbrack - 3\frac{1}{8}; + \infty)\]
\[Убывает\ ( - \infty;\frac{3}{4}\rbrack;\]
\[возрастает\ \ \left\lbrack \frac{3}{4}; + \infty \right).\]
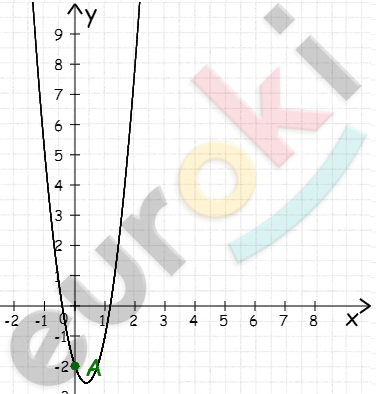
\[8)\ y = - 3x^{2} + 8x + 3\]
\[x_{0} = \frac{- 8}{- 6} = \frac{4}{3} = 1\frac{1}{3},\ \ \]
\[y_{0} = \frac{- 3 \cdot 16}{9} + \frac{32}{3} + 3 = 8\frac{1}{3}\]
\[ветви\ вниз;\]
\[E(y) = \left( - \infty;8\frac{1}{3} \right\rbrack\]
\[Возрастает\ ( - \infty;1\frac{1}{3}\rbrack;\]
\[убывает\ \left\lbrack 1\frac{1}{3}; + \infty \right).\]
