Решебник по алгебре 9 класс Мерзляк Задание 512

 

\[\boxed{\mathbf{512\ (512).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x\ \ цехов\ первого\ типа,\ \]

\[y - цехов\ второго\ типа,\]

\[\ z - цехов\ третьего\ \]

\[типа.\ Тогда\ 350x - рабочих\ в\ \]

\[цехах\ первого\ типа,\ \]

\[80y - в\ цехах\ второго\]

\[типа,\ 60z - рабочих\ в\ цехах\ \]

\[третьего\ типа.\ \]

\[По\ условию\ известно,\ что\ \]

\[всего\ работает\ 980\ человек.\]

\[Составляем\ уравнение:\]

\[350x + 80y + 60z = 980\]

\[Пусть\ x = 1,\ тогда\]

\[\ 350 + 80y + 60z = 980\]

\[80y + 60z = 630 \Longrightarrow таких\]

\[\ целых\ y\ и\ z\ не\ существует.\]

\[Пусть\ x = 2,\ тогда\ 700 +\]

\[+ 80y + 60z = 980\]

\[80y + 60z = 280 \Longrightarrow методом\]

\[\ подбора\ получаем\ y = 2,\ z = 2.\]

\[Следовательно,\ 2\ цеха\]

\[\ каждого\ типа\ на\ заводе.\]

\[Ответ:по\ 2\ цеха.\]

\[\boxed{\text{512.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\text{\ x}^{2} - 8|x| - 33 < 0\]

\[\left\lbrack \begin{matrix} x^{2} - 8x - 33 < 0 \\ x^{2} + 8x - 33 < 0 \\ \end{matrix} \right.\ \]

\[1)\ x^{2} - 8x - 33 < 0\]

\(x_{1} + x_{2} = 8,\ \ \ \ \ \ \ \ \ \ \ x_{1} = - 3\)

\[x_{1}x_{2} = - 33,\ \ x_{2} = 11\]

\[2)\ x^{2} + 8x - 33 < 0\]

\(x_{1} + x_{2} = - 8,\ \ \ \ \ \ \ \ \ \ \ x_{1} = - 11\)

\[x_{1}x_{2} = - 33,\ \ x_{2} = 3\]

\[Ответ:x \in ( - 11;11).\]

\[2)\ 8x^{2} + 7|x| - 1 \geq 0\]

\[\left\lbrack \begin{matrix} 8x^{2} + 7x - 1 \geq 0 \\ 8x^{2} - 7x - 1 \geq 0 \\ \end{matrix} \right.\ \]

\[1)\ 8x^{2} + 7x - 1 \geq 0\]

\[D = 49 + 32 = 81\]

\[x_{1,2} = \frac{- 7 \pm 9}{16}\]

\[x = - 1;\ \ \ x = \frac{1}{8}\]

\[2)\ 8x^{2} - 7x - 1 \geq 0\]

\[D = 49 + 32 = 81\]

\[x_{1,2} = \frac{7 \pm 9}{16}\]

\[x = 1;\ \ x = - \frac{1}{8}\]

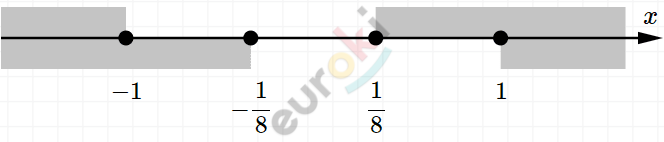
\[Ответ:x \in \left( - \infty;\ - \frac{1}{8} \right\rbrack \cup \left\lbrack \frac{1}{8}; + \infty \right).\]