Решебник по алгебре 9 класс Мерзляк Задание 459

 

\[\boxed{\text{459\ (459).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\left\{ \begin{matrix} y = - 2x - 4\ \ \ \ \ \ \ \ \ \\ y = 6x^{2} - 7x - 2 \\ \end{matrix} \right.\ \]

\[- 2x - 4 = 6x^{2} - 7x - 2\]

\[6x^{2} - 5x + 2 = 0\]

\[D = 25 - 48 < 0;\ \ нет\ решений.\]

\[Следовательно,\]

\[\ графики\ не\ пересекаются.\]

\[2)\left\{ \begin{matrix} y = 4x^{2} - 3x + 6 \\ y = x + 5\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[4x^{2} - 3x + 6 = x + 5\]

\[4x^{2} - 4x + 1 = 0\]

\[D = 16 - 16 = 0\]

\[\left\{ \begin{matrix} x = 0,5 \\ y = 5,5 \\ \end{matrix} \right.\ \]

\[Ответ:одна\ точка\ \]

\[пересечения(0,5;5,5).\]

\[3)\ \left\{ \begin{matrix} y = 4x^{2} - 3x - 24 \\ y = 2x^{2} - 5x\ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\(4x^{2} - 3x - 24 = 2x^{2} - 5x\)

\[2x^{2} + 2x - 24 = 0\ \ |\ :2\]

\[x^{2} + x - 12 = 0\]

\[x_{1} + x_{2} = - 1,\ \ x_{1} = - 4\]

\(x_{1}x_{2} = - 12,\ \ \ \ \ \ \ \ \ \ \ \ x_{2} = 3\)

\[\left\{ \begin{matrix} x = - 4 \\ y = 52 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }или\ \ \ \left\{ \begin{matrix} x = 3 \\ y = 3 \\ \end{matrix} \right.\ \]

\[Ответ:две\ точки\ \]

\[пересечения\ ( - 4;52);\ \ (3;3).\]

\[\boxed{\text{459.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

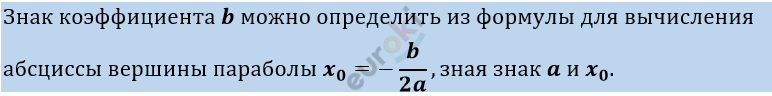
Решение.

\[\mathbf{b = - 2}\mathbf{a}\mathbf{x}_{\mathbf{0}}\mathbf{.}\]

\[1)\ ветви\ вверх:a > 0;\ \ \]

\[x_{0} > 0;\ \ a > 0:\ \ b < 0;\ \ \]

\[y < 0:\ \ c < 0.\]

\[2)\ ветви\ вниз:\ \ \ a < 0;\]

\[x_{0} < 0;x < 0:\ \ \ \ \ b < 0;\ \ \]

\[y > 0:\ \ \ \ c > 0.\]