Решебник по алгебре 9 класс Мерзляк Задание 436
Задание 436



\[\boxed{\text{436\ (436).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1) - x^{2} + 6x - a > 0 \Longrightarrow\]
\[\Longrightarrow ветви\ направлены\ вниз\]
\[D = 36 - 4a\]
\[36 - 4a \leq 0\]
\[a \geq 9\]
\[Ответ:при\ a \geq 9.\]
\[2)\ x^{2} - (a + 1)x + 3a -\]
\[- 5 < 0 \Longrightarrow ветви\ направлены\ \]
\[вверх\]
\[D = (a + 1)^{2} - 4(3a - 5) =\]
\[= a^{2} + 2a + 1 - 12a + 20 =\]
\[= a^{2} - 10a + 21\]
\[a^{2} - 10a + 21 \leq 0\]
\[a_{1} + a_{2} = 10,\ \ a_{1} = 7\]
\[a_{1}a_{2} = 21,\ \ a_{2} = 3\]

\[Ответ:\lbrack 3;7\rbrack.\]
\[3)\ ax^{2} + (a - 1)x +\]
\[+ (a - 1) < 0 \Longrightarrow при\ a > 0\ \]
\[ветви\ направлены\ вверх\]
\[D = (a - 1)^{2} - 4a(a - 1) =\]
\[= a^{2} - 2a + 1 - 4a^{2} + 4a =\]
\[= - 3a^{2} + 2a + 1\]
\[- 3a^{2} + 2a + 1 \leq 0\]
\[D = 4 + 12 = 16\]
\[a_{1} = \frac{- 2 + 4}{- 6} = - \frac{1}{3}\ \]

\[a_{2} = \frac{- 2 - 4}{- 6} = 1\]
\[Ответ:при\ a \geq 1\text{.\ }\]

\[\boxed{\text{436.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1)\ f(x) = - x^{2} + 6x - 7\]
\[x_{0} = \frac{- 6}{- 2} = 3\]
\[y_{0} = - 9 + 18 - 7 = 2\]
\[Oy:\]
\[x = 0;\ \ y = - 7.\]
\[f(1) = - 1 + 6 - 7 = - 2.\]
\[q(x) = - \sqrt{x}\]
| \[x\] | \[1\] | \[4\] | \[9\] |
|---|---|---|---|
| \[y\] | \[- 1\] | \[- 2\] | \[- 3\] |
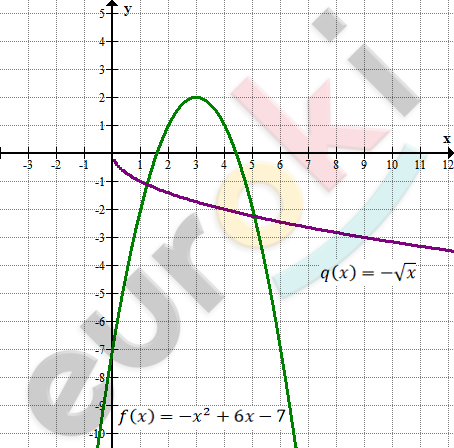
\[Ответ:два\ корня.\]
\[2)\ f(x) = 4x - 2x^{2}\]
\[x_{0} = \frac{- 4}{- 4} = 1;\]
\[y_{0} = 4 - 2 = 2.\]
\[\text{Ox}:\]
\[2x(2 - x) = 0\]
\[x = 0,\ \ (0;0)\]
\[x = 2,\ \ (2;0)\text{.\ }\]
\[\text{Oy}:\ \ \ \]
\[\ y = 0;(0;0).\]
\[f( - 1) = - 4 - 2 = - 6.\]
\[q(x) = - \frac{4}{x}\]
| \[x\] | \[1\] | \[2\] | \[4\] | \[- 1\] | \[- 2\] | \[- 4\] |
|---|---|---|---|---|---|---|
| \[y\] | \[- 4\] | \[- 2\] | \[- 1\] | \[4\] | \[2\] | \[1\] |
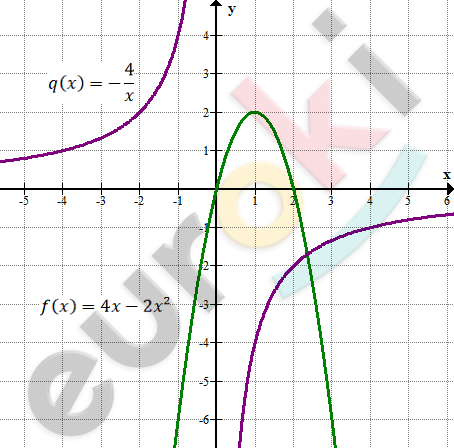
\[Ответ:1\ корень.\]




