Решебник по алгебре 9 класс Мерзляк Задание 423

 

\[\boxed{\text{423\ (423).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Уравнение\ имеет\ два\ \]

\[различных\ корня,\ \]

\[если\ D > 0.\]

\[1)\ x^{2} - 8bx + 15b + 1 = 0\]

\[D = 64b^{2} - 60b - 4\]

\[64b^{2} - 60b - 4 > 0\ \ |\ :4\]

\[16b^{2} - 15b - 1 > 0\]

\[D = 225 + 64 = 289\]

\[b_{1,2} = \frac{15 \pm 17}{32}\]

\[b = - \frac{1}{16};\ \ \ \ b = 1.\]

\[Ответ:b \in \left( - \infty; - \frac{1}{16} \right) \cup (1;\ + \infty).\]

\[2)\ 2x^{2} + 2 \cdot (b - 6)x + b - 2 = 0\]

\[D = 4(b - 6)^{2} - 8(b - 2) =\]

\[= 4b^{2} - 48b + 144 - 8b +\]

\[+ 16 = 4b^{2} - 56b + 160\]

\[4b^{2} - 56b + 160 > 0\ \ |\ :4\]

\[b^{2} - 14b + 40 > 0\]

\[b_{1} + b_{2} = 14,\ \ x_{1} = 10\]

\[b_{1}b_{2} = 40,\ \ x_{2} = 4\]

\[Ответ:b \in ( - \infty;4) \cup (10;\ + \infty).\]

\[\boxed{\text{423.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

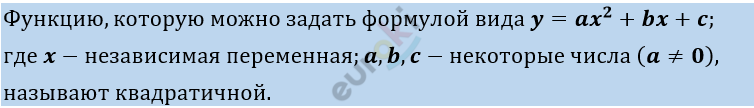
Решение.

\[1)\ y = 4x^{2} + 3x + 6 -\]

\[квадратичная\]

\[2)\ y = 4x + 3 - не\ \]

\[квадратичная\]

\[3)\ y = \frac{1}{2x^{2} - 3x + 2} - не\ \]

\[квадратичная\]

\[4)\ y = 6x^{2} - 5x -\]

\[квадратичная\]