Решебник по алгебре 9 класс Мерзляк Задание 390
Задание 390



\[\boxed{\text{390\ (390).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[y = - 3x^{2} - (3a - 2)x + 2a + 3;\ \ \ \]
\[x_{1} < - 2 < x_{2}\]
\[D = (3a - 2)^{2} + 12(2a + 3) =\]
\[= 9a^{2} - 12a + 4 + 24a + 36 =\]
\[= 9a^{2} + 12a + 40\]
\[x_{1} = \frac{3a - 2 + \sqrt{9a^{2} + 12a + 40}}{- 6}\]
\[x_{2} = \frac{3a - 2 - \sqrt{9a^{2} + 12a + 40}}{- 6}\]
\[\frac{3a - 2 + \sqrt{9a^{2} + 12a + 40}}{- 6} <\]
\[< - 2 <\]
\[< \frac{3a - 2 - \sqrt{9a^{2} + 12a + 40}}{- 6}\]
\[3a - 2 - \sqrt{9a^{2} + 12a + 40} <\]
\[< 12 < 3a - 2 +\]
\[+ \sqrt{9a^{2} + 12a + 40}\]
\[\left\{ \begin{matrix} 3a - 2 - \sqrt{9a^{2} + 12a + 40} < 12 \\ 3a - 2 + \sqrt{9a^{2} + 12a + 40} > 12 \\ \end{matrix} \right.\ \]
\[- \sqrt{9a^{2} + 12a + 40} < - 3a + 14\]
\[\sqrt{9a^{2} + 12a + 40} > 3a - 14\]
\[9a^{2} + 12a + 40 > 9a^{2} -\]
\[- 84a + 196\]
\[96a - 156 > 0\]
\[a > \frac{156}{96}\]
\[a > \frac{13}{8}\]
\[\sqrt{9a^{2} + 12a + 40} > 14 - 3a\]
\[9a^{2} + 12a + 40 > 196 - 84a +\]
\[+ 9a^{2} \Longrightarrow аналогично\ \]
\[неравенству\ \]
\[выше \Longrightarrow a > \frac{13}{8}\]
\[Ответ:\ a > \frac{13}{8}.\]

\[\boxed{\text{390.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
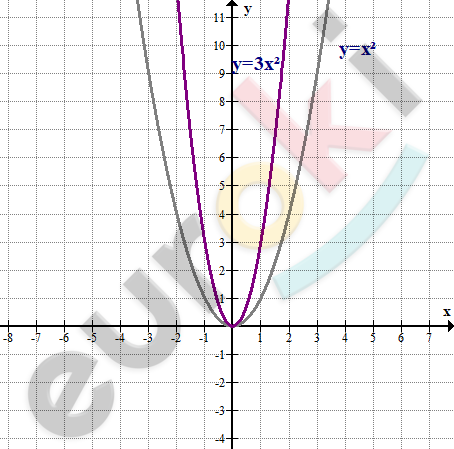
\[1)\ y = 3x^{2},\ расстяжение\ \]
\[графика\ y = x^{2}\ в\ 3\ раза.\]
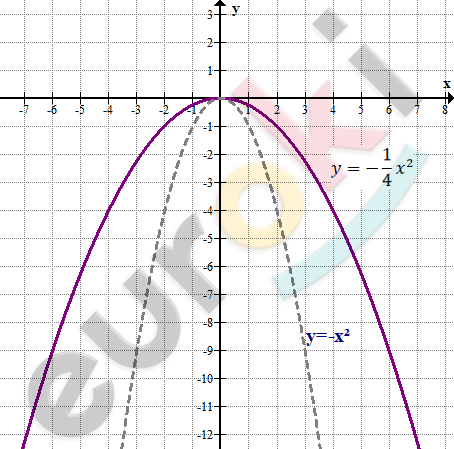
\[2)\ y = - \frac{1}{4}x^{2},\ сжатие\ вдоль\ оси\ \]
\[x\ в\ 4\ раза\ и\ симметрия\ \]
\[относительно\]
\[оси\ x\ графика\ y = x^{2}.\]