Решебник по алгебре 9 класс Мерзляк Задание 283

 

\[\boxed{\text{283\ (283).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\ \frac{км}{ч} - роет\ котлован\ \]

\[первый\ экскаватор,\ \]

\[тогда\ 4x\ \frac{км}{ч} -\]

\[второй\ экскаватор.\ Примем\ за\ \]

\[объем\ котлована - 1.\ \]

\[По\ условию\ \]

\[известно,\ что\ вместе\ \]

\[экскаваторы\ вырыли\ \]

\[котлован\ за\ 8\ ч.\]

\[Составляем\ уравнение:\]

\[(x + 4x) \cdot 8 = 1\]

\[5x \cdot 8 = 1\]

\[40x = 1\]

\[x = \frac{1}{40}\ \left( \frac{км}{ч} \right) - роет\ первый\ \]

\[экскаватор.\]

\[4 \cdot \frac{1}{40} = \frac{1}{10}\ \left( \frac{км}{ч} \right) - роет\ \]

\[второй\ экскаватор.\]

\[1\ :\frac{1}{40} = 40\ (ч) - время\ работы\ \]

\[первого\ экскаватора.\]

\[1\ :\frac{1}{10} = 10\ (ч) - время\ работы\ \]

\[второго\ экскаватора.\]

\[Ответ:10\ ч;40\ ч.\ \]

\[\boxed{\text{283.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ |x + 5| - 3x > 4\]

\[|x + 5| > 4 + 3x\]

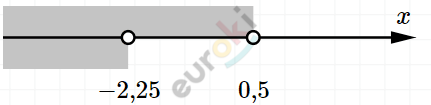
\[Ответ:x \in ( - \infty;0,5).\]

\[2)\ |x - 1| + x \leq 3\]

\[|x - 1| \leq 3 - x\]

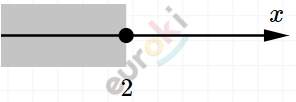
\[Ответ:x \in ( - \infty;2\rbrack\text{.\ \ }\]