Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Мерзляк Задание 168
Задание 168
\[\boxed{\text{168\ (168).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[Пусть\ \text{x\ }часов\ требуется,\ чтобы\ \]
\[наполнить\ бассейн\ \]
\[через\ 1\ трубу,\]
\[а\ 1,5x\ ч - через\ вторую\ трубу.\ \]
\[По\ условию\ известно,\ что\ \]
\[одновременно\]
\[две\ трубы\ наполнят\ бассейн\ \]
\[за\ 6\ часов.\]
\[Составляем\ уравнение:\]
\[\frac{1}{x} + \frac{1}{1,5x} = \frac{1}{6}\]
\[\frac{1,5 + 1}{1,5x} = \frac{1}{6}\]
\[15 = 1,5x\]
\[x = 10\ (ч) - требуется\ \]
\[первой\ трубе.\]
\[1,5 \cdot 10 = 15\ (ч) - требуется\ \]
\[второй\ трубе.\]
\[Ответ:10\ ч,\ 15\ ч.\]
\[\boxed{\text{168.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1)\left\{ \begin{matrix} x^{2} + y^{2} = 3 \\ y = \text{x\ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[x^{2} + y^{2} = 3\]
\[O\ (0;0),\ \ r = \sqrt{3} \approx 1,7\]
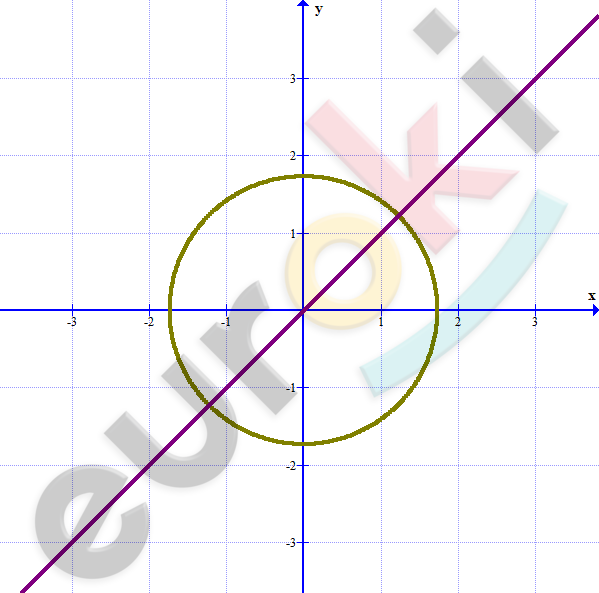
\[Ответ:2\ решения.\]
\[2)\ \left\{ \begin{matrix} y = \sqrt{x}\text{\ \ \ \ } \\ x - y = 2 \\ \end{matrix} \right.\ \]
\[y = \sqrt{x}\]
| \[x\] | \[9\] | \[4\] | \[1\] | \[0\] |
|---|---|---|---|---|
| \[y\] | \[3\] | \[2\] | \[1\] | \[0\] |
\[y = x - 2\]
| \[x\] | \[0\] | \[2\] |
|---|---|---|
| \[y\] | \[- 2\] | \[0\] |
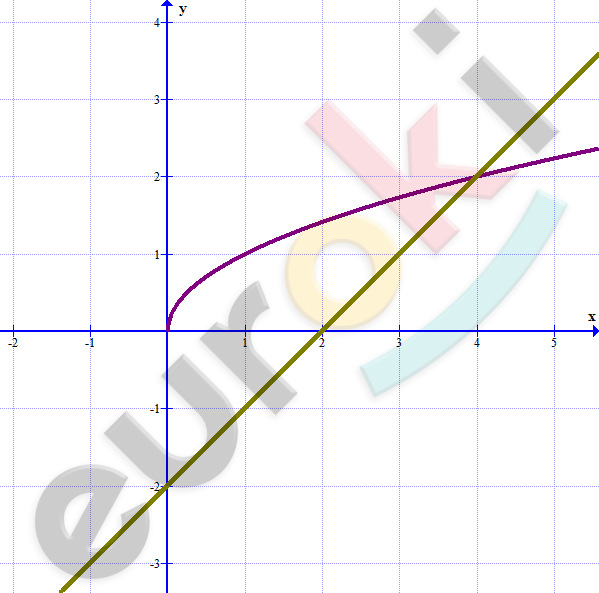
\[Ответ:1\ решение.\]
\[3)\ \left\{ \begin{matrix} xy = - 6\ \ \ \ \\ 2x - y = 3 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\left\{ \begin{matrix} y = - \frac{6}{x}\text{\ \ \ \ \ \ } \\ y = 2x - 3 \\ \end{matrix} \right.\ \]
\[y = - \frac{6}{x}\]
| \[x\] | \[6\] | \[3\] | \[2\] | \[1\] | \[- 6\] | \[- 3\] | \[- 2\] | \[- 1\] |
|---|---|---|---|---|---|---|---|---|
| \[y\] | \[- 1\] | \[- 2\] | \[- 3\] | \[- 6\] | \[1\] | \[2\] | \[3\] | \[6\] |
\[y = 2x - 3\ \]
| \[x\] | \[0\] | \[2\] |
|---|---|---|
| \[y\] | \[- 3\] | \[1\] |
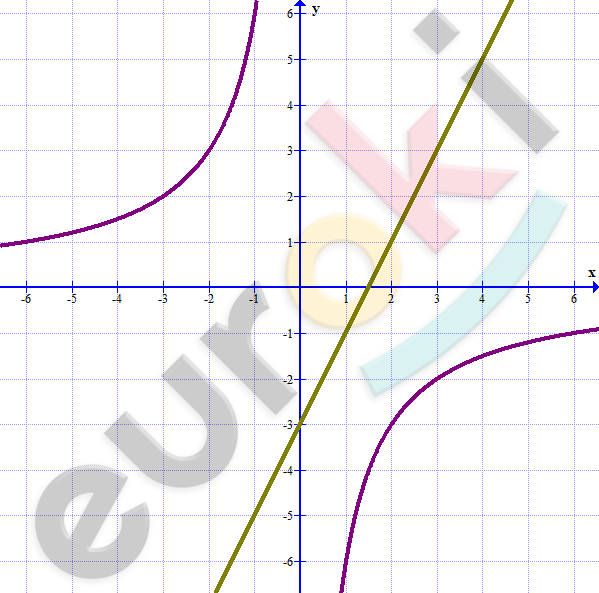
\[Ответ:нет\ решений.\]
