Решебник по алгебре 9 класс Рурукин контрольные работы КР-4. Уравнения и неравенства с двумя переменными Вариант 6

Условие:

1. Решите систему уравнений

\[\left\{ \begin{matrix} x^{2} - y^{2} = 3(x + y) \\ \frac{1}{4x - 3y} = \frac{1}{7}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]

2. Найдите решение системы уравнений

\[\left\{ \begin{matrix} 3\sqrt{\frac{x}{y}} + 2\sqrt{\frac{y}{x}} = 5 \\ 4\sqrt{x} + \sqrt{y} = 10 \\ \end{matrix} \right.\ \]

3. Найдите все пары (x; y) целых чисел x и y, являющихся решениями системы уравнений.

\[\left\{ \begin{matrix} x = \frac{7y - 34}{y - 5}\text{\ \ } \\ x^{2} + y^{2} = 52 \\ \end{matrix} \right.\ \]

4. Если велосипедист увеличит скорость на 5 км/ч, то получит выигрыш во времени 12 мин при прохождении некоторого пути. Если же он уменьшит скорость на 8 км/ч, то потеряет 40 мин на том же пути. Найдите скорость велосипедиста и длину пути.

5. Изобразите на координатной плоскости множество решений уравнения |y²-x²|=y+x.

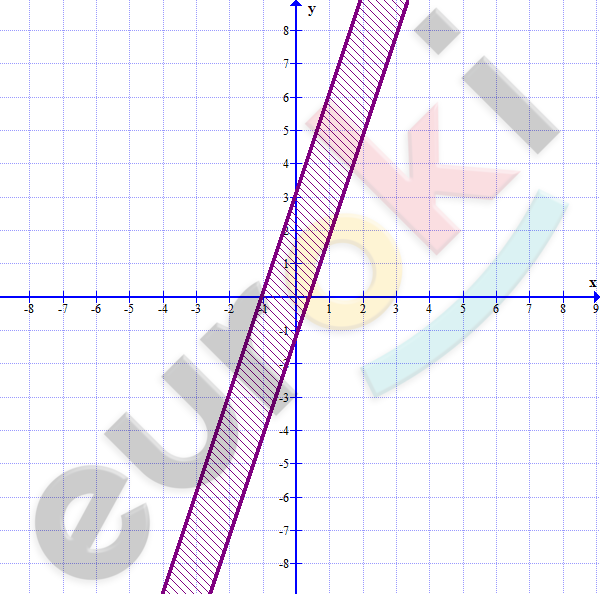
6. На координатной плоскости изобразите множество решений неравенства

|3x-y+1|<=2.

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[\left\{ \begin{matrix} x^{2} - y^{2} = 3(x + y) \\ \frac{1}{4x - 3y} = \frac{1}{7}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\left\{ \begin{matrix} (x + y)(x - y - 3) = 0 \\ 4x - 3y = 7\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1)\ \left\{ \begin{matrix} x + y = 0\ \ \ \ \ \\ 4x - 3y = 7 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} x = - y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 4 \cdot ( - y) - 3y = 7 \\ \end{matrix} \right.\ \]

\[- 4y - 3y = 7\]

\[- 7y = 7\]

\[y = - 1 \Longrightarrow x = 1.\]

\[2)\ \left\{ \begin{matrix} x - y = 3\ \ \ \ \ \\ 4x - 3y = 7 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} x = 3 + y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 4(3 + y) - 3y = 7 \\ \end{matrix} \right.\ \]

\[12 + 4y - 3y = 7\]

\[y = 7 - 12\]

\[y = - 5 \Longrightarrow x = 3 - 5 = - 2.\]

\[Ответ:(1;\ - 1);( - 2; - 5).\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[\left\{ \begin{matrix} 3\sqrt{\frac{x}{y}} + 2\sqrt{\frac{y}{x}} = 5 \\ 4\sqrt{x} + \sqrt{y} = 10 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\sqrt{\frac{x}{y}} = t:\]

\[3t + \frac{2}{t} = 5\]

\[3t^{2} + 2 - 5t = 0\]

\[3t^{2} - 5t + 2 = 0\]

\[D = 25 - 24 = 1\]

\[1)\ \left\{ \begin{matrix} \sqrt{\frac{x}{y}} = 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 4\sqrt{x} + \sqrt{y} = 10 \\ \end{matrix} \right.\ \ \]

\[\left\{ \begin{matrix} \sqrt{x} = \sqrt{\text{y\ }}\text{\ \ \ \ \ \ \ \ \ \ \ \ } \\ 4\sqrt{x} + \sqrt{y} = 10 \\ \end{matrix} \right.\ \]

\[4\sqrt{y} + \sqrt{y} = 10\]

\[5\sqrt{y} = 10\]

\[\sqrt{y} = 2 \Longrightarrow y = 4.\]

\[\sqrt{x} = 2 \Longrightarrow x = 4.\]

\[2)\ \left\{ \begin{matrix} \sqrt{\frac{x}{y}} = \frac{2}{3}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ 4\sqrt{x} + \sqrt{y} = 10 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \sqrt{x} = \frac{2}{3}\sqrt{y}\text{\ \ \ \ \ \ \ \ \ } \\ 4\sqrt{x} + \sqrt{y} = 10 \\ \end{matrix} \right.\ \ \]

\[4 \cdot \frac{2}{3}\sqrt{y} + \sqrt{y} = 10\]

\[\frac{8}{3}\sqrt{y} + \sqrt{y} = 10\]

\[\frac{11\sqrt{y}}{3} = 10\]

\[\sqrt{y} = \frac{30}{11} \Longrightarrow y = \frac{900}{121};\]

\[\sqrt{x} = \frac{2}{3} \cdot \frac{30}{11} = \frac{20}{11} \Longrightarrow x = \frac{400}{121}.\]

\[Ответ:(4;4);\left( \frac{400}{121};\frac{900}{121} \right).\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[\left\{ \begin{matrix} x = \frac{7y - 34}{y - 5}\text{\ \ } \\ x^{2} + y^{2} = 52 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[x = \frac{7y - 35 + 1}{y - 5} = 7 + \frac{1}{y - 5}\]

\[1)\ y - 5 = 1:\]

\[y = 6 \Longrightarrow x = 8.\]

\[2)\ y - 5 = - 1:\]

\[y = 4 \Longrightarrow x = 6.\]

\[Подставим:\]

\[1)\ (6;4):\]

\[x^{2} + y^{2} = 52\]

\[36 + 16 = 52.\]

\[2)\ (8;1):\]

\[x^{2} + y^{2} = 52\]

\[64 + 1 = 52\]

\[65 \neq 52.\]

\[Ответ:(6;4).\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[Пусть\ \text{x\ }\frac{км}{ч} - скорость\ \]

\[велосипедиста;\]

\[\text{y\ }км - расстояние.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} \frac{y}{x} - \frac{y}{x + 5} = \frac{12}{60} \\ \frac{y}{x - 8} - \frac{y}{x} = \frac{40}{60} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 25y = x(x + 5) \\ 12y = x(x - 8) \\ \end{matrix} \right.\ \ \ (\ :)\]

\[\frac{25}{12} = \frac{x + 5}{x - 8}\]

\[25 \cdot (x - 8) = 12(x + 5)\]

\[25x - 200 = 12x + 60\]

\[25x - 12x = 60 + 200\]

\[13x = 260\]

\[x = 20\ \left( \frac{км}{ч} \right) - скорость\ \]

\[велосипедиста.\]

\[y = \frac{x(x + 5)}{25} = \frac{25(25 + 5)}{25} =\]

\[= 30\ (км) - расстояние.\ \]

\[Ответ:20\ \frac{км}{ч};30\ км.\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[\left| y^{2} - x^{2} \right| = y + x\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[|3x - y + 1| \leq 2\]