Решебник по алгебре 9 класс Рурукин контрольные работы КР-3. Уравнения и неравенства с одной переменной Вариант 2

Условие:

1. Решите уравнение 4x^2 (1-x)=1-x.

2. Найдите корни уравнения 3/(x^2+4x)-15/(x^2-4x)=4/x.

3. Решите неравенство (x+2)(3x-6)(2x+9)≤0.

4. Найдите решение неравенства 4/(x-2)≥7/(x-3).

5. При каких значениях параметра a уравнение 4x²+3ax+1=0 имеет два различных корня?

6. Решите неравенство (3-4x)^2 (3x+2)≤0.

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\(4x^{2}(1 - x) = 1 - x\)

\[1 - x = 0\]

\[x = 1.\]

\[4x^{2} = 1\]

\[x^{2} = \frac{1}{4}\]

\[x = \pm \frac{1}{2}.\]

\[Ответ:x = 1;\ \ x = \pm \frac{1}{2}.\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[\frac{3}{x^{2} + 4x} - \frac{15}{x^{2} - 4x} = \frac{4}{x}\]

\[\frac{3^{\backslash x - 4}}{x(x + 4)} - \frac{15^{\backslash x + 4}}{x(x - 4)} = \frac{4^{\backslash x^{2} - 16}}{x}\]

\[\frac{3x - 12 - 15x - 60 - 4x^{2} + 64}{x\left( x^{2} - 16 \right)} = 0\]

\[ОДЗ:\ \ x \neq 0;\ \ \ x \neq \pm 4\]

\[- 4x^{2} - 12x - 8 = 0\ \ \ \ \ |\ :( - 4)\]

\[x^{2} + 3x + 2 = 0\]

\[D = 9 - 8 = 1\]

\[x_{1} = \frac{- 3 + 1}{2} = - 1;\ \ \ \]

\[x_{2} = \frac{- 3 - 1}{2} = - 2\]

\[Ответ:x = - 1;x = - 2.\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[(x + 2)(3x - 6)(2x + 9) \leq 0\]

\[x = - 2;\ \ x = 2;\ \ x = - 4,5\]

\[Ответ:x \in ( - \infty; - 4,5\rbrack \cup \lbrack - 2;2\rbrack.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[\frac{4^{\backslash x - 3}}{x - 2} \geq \frac{7^{\backslash x - 2}}{x - 3}\]

\[\frac{4x - 12 - 7x + 14}{(x - 2)(x - 3)} \geq 0\]

\[\frac{- 3x + 2}{(x - 2)(x - 3)} \geq 0\]

\[x = \frac{2}{3};\ \ x = 2;\ \ x = 3\]

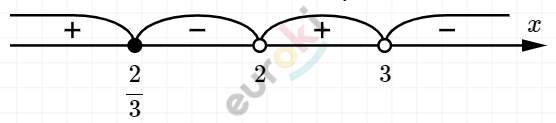
\[Ответ:x \in \left( - \infty;\frac{2}{3} \right\rbrack \cup (2;3).\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[4x^{2} + 3ax + 1 = 0\]

\(Уравнение\ имеет\ два\ \)

\[различных\ корня,если\ D > 0.\]

\[D = 9a^{2} - 16\]

\[9a^{2} - 16 > 0\]

\[(3a + 4)(3a - 4) > 0\]

\[a = - \frac{4}{3};\ \ a = \frac{4}{3}\]

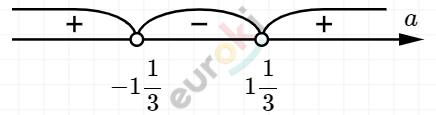
\[Ответ:\]

\[при\ a \in \left( - \infty; - 1\frac{1}{3} \right) \cup \left( 1\frac{1}{3}; + \infty \right).\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[(3 - 4x)^{2}(3x + 2) \leq 0\]

\[(3x + 2)(3 - 4x)(3 - 4x) \leq 0\]

\[x = \frac{3}{4};\ \ x = - \frac{2}{3}\]

\[Ответ:x \in \left( - \infty; - \frac{2}{3} \right\rbrack \cup \left\{ 0,75 \right\}.\]