Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Рурукин контрольные работы КР-4. Уравнения и неравенства с двумя переменными Вариант 1
Вариант 1
Условие:
1. Решите систему уравнений способом сложения.
\[\left\{ \begin{matrix} 3x + y = 7\ \ \\ 2x^{2} - y = 7 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]
2. Решите систему уравнений способом подстановки.
\[\left\{ \begin{matrix} 4x - y = 2\ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + y^{2} - xy = 3 \\ \end{matrix} \right.\ \]
3. Периметр прямоугольника равен 28 см, а его площадь равна 40 см².Найдите стороны прямоугольника.
4. Найдите двузначное число, которое в три раза больше суммы своих цифр.
5. Изобразите на координатной плоскости множество решений неравенства (x+1)²+(y-2)²<=4. Вычислите площадь полученной фигуры.
6. Изобразите на координатной плоскости множество решений системы неравенств. Найдите площадь полученной фигуры.
\[\left\{ \begin{matrix} x^{2} + y^{2} \leq 16\ \\ y \geq x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]
\[\left\{ \begin{matrix} 3x + y = 7\ \ \\ 2x^{2} - y = 7 \\ \end{matrix} \right.\ \ ( + )\text{\ \ \ \ \ }\]
\[\left\{ \begin{matrix} 3x + 2x^{2} = 14 \\ y = 7 - 3x\ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} 2x^{2} + 3x - 14 = 0 \\ y = 7 - 3x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[2x^{2} + 3x - 14 = 0\]
\[D = 9 + 112 = 121\]
\[x_{1} = \frac{- 3 + 11}{4} = 2;\ \ \]
\[y_{1} = 7 - 3 \cdot 2 = 1\ \]
\[x_{2} = \frac{- 3 - 11}{4} = - \frac{14}{4} = - 3,5;\]
\[y_{2} = 7 - 3 \cdot ( - 3,5) =\]
\[= 7 + 10,5 = 17,5.\]
\[\left\{ \begin{matrix} x = 2 \\ y = 1 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} x = - 3,5\ \ \\ y = 17,5\ \ \ \\ \end{matrix} \right.\ \ \]
\[Ответ:(2;1);( - 3,5;\ 17,5).\]
\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]
\[\left\{ \begin{matrix} 4x - y = 2\ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + y^{2} - xy = 3 \\ \end{matrix} \right.\ \text{\ \ \ \ }\]
\[\ \left\{ \begin{matrix} y = 4x - 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + (4x - 2)^{2} - x(4x - 2) = 3\ (*) \\ \end{matrix} \right.\ \]
\[(*):\]
\[x^{2} + 16x^{2} - 16x + 4 - 4x^{2} + 2x - 3 = 0\]
\[13x^{2} - 14x + 1 = 0\]
\[D = 49 - 13 = 36\]
\[x_{1} = \frac{7 + 6}{13} = 1;\ \ \]
\[x_{2} = \frac{7 - 6}{13} = \frac{1}{13}\]
\[y_{2} = 4 \cdot \frac{1}{13} - 2 =\]
\[= \frac{4}{13} - 2 = - 1\frac{9}{13}\]
\[y_{1} = 4 \cdot 1 - 2 = 2\]
\[\left\{ \begin{matrix} x = \frac{1}{13}\text{\ \ \ \ } \\ y = 1\frac{9}{13} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} x = 1 \\ y = 2 \\ \end{matrix} \right.\ \]
\[Ответ:\left( \frac{1}{13};1\frac{9}{13} \right);(1;\ 2).\]
\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]
\[Пусть\ \text{a\ }и\ b - стороны\ \]
\[прямоугольника.\]
\[Известно,\ что\ периметр\ \]
\[28\ см,\ а\ площадь\ 40\ см^{2}.\]
\[Составим\ систему\ уравнений:\]
\[\left\{ \begin{matrix} 2(a + b) = 28 \\ ab = 40\ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} a + b = 14 \\ ab = 40\ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ }\]
\[\left\{ \begin{matrix} a = 14 - b\ \ \ \ \ \ \ \\ (14 - b)b = 40 \\ \end{matrix} \right.\ \]
\(14b - b^{2} = 40\)
\[b^{2} - 14b + 40 = 0\]
\[D = 49 - 40 = 9\]
\[b_{1} = 7 + 3 = 10\ \]
\[b_{2} = 7 - 3 = 4\]
\[\left\{ \begin{matrix} b = 10 \\ a = 4\ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\left\{ \begin{matrix} b = 4\ \ \ \\ a = 10 \\ \end{matrix} \right.\ \]
\[Ответ:4\ см\ и\ 10\ см.\]
\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]
\[Пусть\ x - число\ десятков,\ \]
\[y - число\ единиц.\]
\[Составим\ уравнение:\]
\[10x + y = 3(x + y)\]
\[10x + y = 3x + 3y\]
\[10x - 3x = 3y - y\]
\[7x = 2y\]
\[x = 2;\ \ y = 7.\]
\[Ответ:число\ 27.\]
\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]
\[(x + 1)^{2} + (y - 2)^{2} \leq 4\]
\[Получили\ круг\ с\ радиусом = 2.\]
\[S = \pi r^{2} = 2^{2}\pi = 4\pi.\]
\[Ответ:круг;\ 4\pi.\]
\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]
\[\left\{ \begin{matrix} x^{2} + y^{2} \leq 16\ \\ y \geq x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \ \]
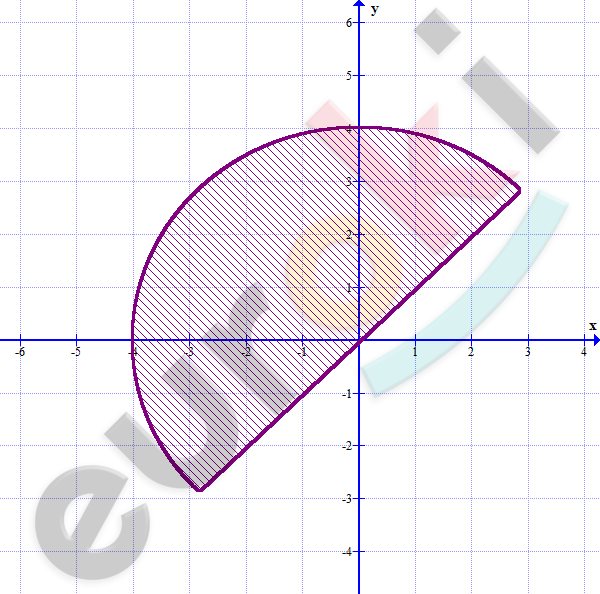
\[Получили\ полукруг,\ с\ \]
\[радиусом = 4.\]
\[S = \frac{\pi \cdot 4^{2}}{2} = \frac{16\pi}{2} = 8\pi.\]
\[Ответ:полукруг;8\pi.\]
