Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Мерзляк контрольные работы КР-6. Обобщение и систематизация знаний учащихся Вариант 4.
Вариант 4.
Условие:
1. Решите неравенство 2x-3(x+4)<x-16.
2. Постройте график функции f (x) =x ^2 – 4 x + 3. Пользуясь графиком, найдите:
1) промежуток возрастания функции;
2) множество решений неравенства x^2 – 4x + 3 < 0.
3. Решите систему уравнений
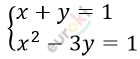
4. Найдите сумму первых шести членов арифметической прогрессии, если её третий член равен 54, а пятый равен 6.
5. Если открыть одновременно две трубы, то бассейн будет наполнен водой за 8 ч. Если сначала наполнять бассейн только через одну трубу в течение 12 ч, а потом только через другую в течение 3 ч, то водой наполнено 3/4 бассейна. За сколько часов может быть наполнен бассейн через каждую трубу?
6. При каких значениях a уравнение x^2 – (a – 5)x + 9 = 0 имеет два различных корня?
7. На четырёх карточках записаны числа 3, 6, 9 и 14. Какова вероятность того, что произведение чисел, записанных на двух наугад выбранных карточках, не будет кратным числу 9?
Решение:
\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]
\[2x - 3(x + 4) < x - 16\]
\[2x - 3x - 12 - x < - 16\]
\[- 2x < - 16 + 12\]
\[- 2x < - 4\]
\[x > 2.\]
\[Ответ:x > 2.\]
\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]
\[f(x) = x^{2} - 4x + 3\]
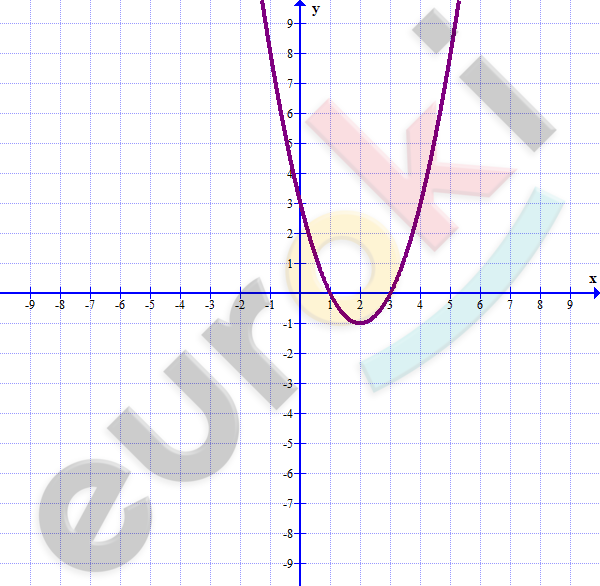
\[1)\ функция\ возрастает\ на\ \]
\[промежутке\ x \in (2; + \infty).\]
\[2)\ x^{2} - 4x + 3 \leq 0\]
\[x \in \lbrack 1;3\rbrack.\]
\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]
\[\left\{ \begin{matrix} x + y = 1\ \ \ \ \ \\ x^{2} - 3y = 1 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]
\[\left\{ \begin{matrix} y = 1 - x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} - 3(1 - x) = 1 \\ \end{matrix} \right.\ \]
\[x^{2} - 3 + 3x - 1 = 0\]
\[x^{2} + 3x - 4 = 0\]
\[x_{1} + x_{2} = - 3;\ \ x_{1} \cdot x_{2} = - 4\]
\[x_{1} = - 4;\ \ \ x_{2} = 1.\]
\[\left\{ \begin{matrix} x = - 4\ \ \ \ \\ y = 1 + 4 \\ \end{matrix} \right.\ \ \ \ \ или\ \ \ \ \left\{ \begin{matrix} x = 1\ \ \ \ \ \ \ \ \\ y = 1 - 1 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = - 4 \\ y = 5\ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x = 1 \\ y = 0 \\ \end{matrix} \right.\ \]
\[Ответ:( - 4;5)\ или\ (1;0).\]
\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]
\[a_{3} = 54;\ \ a_{5} = 6.\]
\[a_{3} = a_{1} + 2d = 54 \rightarrow a_{1} = 54 - 2d;\]
\[a_{5} = a_{1} + 4d = 6 \rightarrow a_{1} = 6 - 4d.\]
\[54 - 2d = 6 - 4d\]
\[- 2d + 4d = 6 - 54\]
\[2d = - 48\]
\[d = - 24.\]
\[a_{1} = 54 - 2 \cdot ( - 24) =\]
\[= 54 + 48 = 102.\]
\[a_{6} = a_{5} + d = 6 - 24 = - 18.\]
\[S_{6} = \frac{(102 - 18) \cdot 6}{2} =\]
\[= 84 \cdot 3 = 252.\]
\[Ответ:252.\]
\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]
\[Пусть\ x - производительность\ \ \]
\[первой\ трубы;тогда\]
\[y - производительность\ \]
\[второй.\]
\[1 - весь\ бассейн.\]
\[Составим\ систему\ уравнений:\]
\[\left\{ \begin{matrix} (x + y) \cdot 8 = 1 \\ 12x + 3y = \frac{3}{4}\text{\ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]
\[\left\{ \begin{matrix} x + y = \frac{1}{8}\ \ \ \ \ \ \ \ | \cdot 24 \\ 12x + 3y = \frac{3}{4}\ \ \ | \cdot 8 \\ \end{matrix} \right.\ \]
\[\ \left\{ \begin{matrix} 24x + 24y = 3 \\ 96x + 24y = 6 \\ \end{matrix} \right.\ \ ( - )\]
\[- 72x = - 3\]
\[x = \frac{3}{72} = \frac{1}{24}.\]
\[24\ (ч) - надо\ первой\ трубе.\]
\[y = \frac{1}{8} - \frac{1}{24} = \frac{3}{24} - \frac{1}{24} = \frac{2}{24} = \frac{1}{12}.\]
\[12\ (ч) - надо\ второй\ трубе.\]
\[Ответ:24\ ч\ и\ 12\ ч.\]
\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]
\[x^{2} - (a - 5)x + 9 = 0\]
\[Уравнение\ имеет\ два\ \]
\[различных\ корня\ при\ D > 0.\]
\[D = (a - 5)^{2} - 4 \cdot 9 =\]
\[= a^{2} - 10a + 25 - 36 =\]
\[= \ a^{2} - 10a - 11\]
\[a^{2} - 10a - 11 > 0\]
\[a_{1} + a_{2} = 10;\ \ a_{1} \cdot a_{2} = - 11\]
\[a_{1} = 11;\ \ \ \ a_{2} = - 1.\]
\[(a + 1)(a - 11) > 0\]
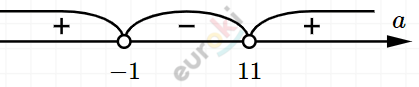
\[a < - 1;\ \ a > 11.\]
\[Ответ:при\ a < - 1;a > 11.\]
\[\boxed{\mathbf{7}\mathbf{.}\mathbf{\ }}\]
\[Существует\ 6\ равновозможных\ \]
\[исходов:\]
\[3 \cdot 6 = 18;\]
\[3 \cdot 9 = 27;\]
\[3 \cdot 14 = 42;\]
\[6 \cdot 9 = 54;\]
\[6 \cdot 14 = 84;\]
\[9 \cdot 14 = 126.\]
\[Из\ них\ благопрятными\ \]
\[являются\ 2.\]
\[Вероятность\ равна:\]
\[\frac{6}{2} = \frac{1}{3}.\]
\[Ответ:\ \frac{1}{3}\text{.\ \ }\]
