Решебник по алгебре 9 класс Макарычев контрольные работы КР-4. Неравенства с одной переменной Вариант 2

Условие:

1. Решите неравенство:

а) 81 – x² > 0;

б) 6x² – x – 1 < 0;

в) 5x² + 3x + 2 > 0.

2. При каких значениях x трёхчлен x² + x – 56 принимает положительные значения?

3. Используя метод интервалов, решите неравенство (x – 16)(x + 7)(x + 1) > 0.

4. При каких значениях p уравнение 10x² + px + 40 = 0 не имеет корней?

5. Найдите область определения функции:

а) y=√(13x-5x²)

б) y=√(x^2+4x-5)/(3x-4)

\[\boxed{\mathbf{1.}\mathbf{\ }}\]

\[\textbf{а)}\ 81 - x^{2} > 0\]

\[x^{2} - 81 < 0\]

\[(x + 9)(x - 9) < 0\]

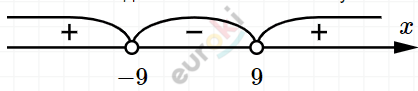
\[x \in ( - 9;9).\]

\[\textbf{б)}\ 6x^{2} - x - 1 < 0\]

\[6x^{2} - x - 1 = 0\]

\[D = 1 + 24 = 25\]

\[x_{1} = \frac{1 + 5}{12} = \frac{1}{2} = 0,5;\]

\[x_{2} = \frac{1 - 5}{12} = - \frac{4}{12} = - \frac{1}{3}.\]

\[6\left( x + \frac{1}{3} \right)(x - 0,5) < 0\]

\[x \in \left( - \frac{1}{3};0,5 \right).\]

\[\textbf{в)}\ 5x^{2} + 3x + 2 > 0\ \]

\[5x^{2} + 3x + 2 = 0\]

\[D = 9 - 40 = - 31 < 0\]

\[Так\ как\ a = 5 > 0;\]

\[ветви\ вверх,\ тогда\ \]

\[x \in ( - \infty; + \infty).\]

\[\boxed{\mathbf{2.}\mathbf{\ }}\]

\[x^{2} + x - 56 > 0\]

\[x^{2} + x - 56 = 0\]

\[По\ теореме\ Виета:\]

\[x_{1} + x_{2} = - 1;\ \ x_{1} \cdot x_{2} = - 56\]

\[x_{1} = - 8;\ \ x_{2} = 7.\]

\[(x + 8)(x - 7) > 0\]

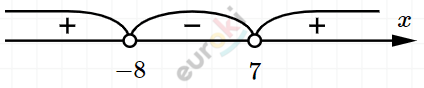
\[При\ x \in ( - \infty; - 8) \cup (7; + \infty).\]

\[\boxed{\mathbf{3.}\mathbf{\ }}\]

\[(x - 16)(x + 7)(x + 1) > 0\]

\[x = - 7;\ \ x = - 1;\ \ x = 16\]

\[x \in ( - 7;\ - 1) \cup (16; + \infty).\]

\[\boxed{\mathbf{4.}\mathbf{\ }}\]

\[10x^{2} + px + 40 = 0\]

\[Уравнение\ не\ имеет\ корней\ \]

\[при\ D < 0.\]

\[D = p^{2} - 1600\]

\[p^{2} - 1600 < 0\]

\[(p + 40)(p - 40) < 0\]

\[p \in ( - 40;40).\]

\[\boxed{\mathbf{5.}\mathbf{\ }}\]

\[\textbf{а)}\ y = \sqrt{13x - 5x²}\]

\[13x - 5x^{2} \geq 0\]

\[5x^{2} - 13x \leq 0\]

\[5x(x - 2,6) \leq 0\]

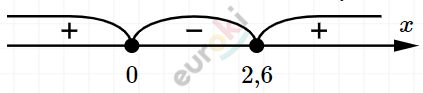
\[x \in \lbrack 0;2,6\rbrack.\]

\[\textbf{б)}\ y = \frac{\sqrt{x^{2} + 4x - 5}}{3x - 4}\ \]

\[3x - 4 \neq 0\]

\[3x \neq 4\]

\[x \neq \frac{4}{3} \neq 1\frac{1}{3}.\]

\[x^{2} + 4x - 5 \geq 0\]

\[D = 4 + 5 = 9\]

\[x_{1} = - 2 + 3 = 1;\]

\[x_{2} = - 2 - 3 = - 5\]

\[(x + 5)(x - 1) \geq 0\]

\[Но\ x \neq 1\frac{1}{3}:\]

\[x \in ( - \infty; - 5\rbrack \cup \left\lbrack 1;1\frac{1}{3} \right) \cup \left( 1\frac{1}{3}; + \infty \right).\]

## КР-5. Уравнения и неравенства с двумя переменными