Решебник по алгебре 9 класс Макарычев контрольные работы КР-3. Уравнения с одной переменной Вариант 2

Условие:

1. При каких значениях x равно нулю значение выражения:

а) x^3-169x

б) (x^2+15x-76)/(2x+38)

в) (3x^2+11x-42)/(x^2-36)

2. Решите биквадратное уравнение:

а) x^4 – 17x² + 16 = 0;

б) 16x^4– 25x² + 9 = 0.

3. Найдите координаты точек пересечения графика функции y = x^4 – 4x² – 45 с осями координат.

4. Решите уравнение

(2x-10)/(x^2-3x)-(x+4)/(x^2+3x)=2/(9-x^2 ).

5. Найдите координаты точек пересечения графиков функций

y=x^3/(x-1) и y=x^2+3x-2.

\[\boxed{\mathbf{1.}\mathbf{\ }}\]

\[\textbf{а)}\ x^{3} - 169x\]

\[x\left( x^{2} - 169 \right) = 0\]

\[x(x - 13)(x + 13) = 0\]

\[x = 0;\ \ x = 13;\ \ x = - 13.\]

\[Ответ:при\ x = 0;\ \ x = \pm 13.\]

\[\textbf{б)}\ \frac{x^{2} + 15x - 76}{2x + 38}\]

\[2x + 38 \neq 0\]

\[2x \neq - 38\]

\[x \neq - 19.\]

\[x^{2} + 15x - 76 = 0\]

\[x_{1} + x_{2} = - 15;\ \ x_{1} \cdot x_{2} = - 76\]

\[x_{1} = 4;\ \ \ \]

\[x_{2} = - 19\ (не\ подходит).\]

\[Ответ:при\ x = 4.\]

\[\textbf{в)}\ \frac{3x^{2} + 11x - 42}{x^{2} - 36}\]

\[x^{2} - 36 \neq 0\]

\[x^{2} \neq 36\]

\[x \neq \pm 6.\]

\[3x^{2} + 11x - 42 = 0\]

\[D = 121 + 504 = 625\]

\[x_{1} = \frac{- 11 + 25}{6} = \frac{14}{6} = 2\frac{2}{6} = 2\frac{1}{3};\]

\[x_{2} = \frac{- 11 - 25}{6} = - 6\ (не\ подходит).\]

\[Ответ:при\ x = 2\frac{1}{3}.\]

\[\boxed{\mathbf{2.}\mathbf{\ }}\]

\[\textbf{а)}\ x^{4} - 17x^{2} + 16 = 0\]

\[Пусть\ x^{2} = y \geq 0:\]

\[y^{2} - 17y + 16 = 0\]

\[y_{1} + y_{2} = 17;\ \ \ y_{1} \cdot y_{2} = 16\]

\[y_{1} = 1;\ \ y_{2} = 16.\]

\[Подставим:\]

\[1)\ y = 1:\]

\[x^{2} = 1\]

\[x = \pm 1.\]

\[2)\ y = 16:\]

\[x^{2} = 16\]

\[x = \pm 4.\]

\[Ответ:\ \ x = \pm 1;\ \ x = \pm 4.\]

\[\textbf{б)}\ 16x^{4} - 25x^{2} + 9 = 0\]

\[Пусть\ x^{2} = y:\]

\[16y^{2} - 25y + 9 = 0\]

\[D = 625 - 576 = 49\]

\[y_{1} = \frac{25 + 7}{32} = 1;\]

\[y_{2} = \frac{25 - 7}{32} = \frac{18}{32} = \frac{9}{16}.\]

\[Подставим:\]

\[1)\ y = 1:\]

\[x^{2} = 1\]

\[x = \pm 1.\]

\[2)\ y = \frac{9}{16}:\]

\[x^{2} = \frac{9}{16}\]

\[x = \pm \frac{3}{4}.\]

\[Ответ:\ \ x = \pm 1;\ \ x = \pm \frac{3}{4}.\]

\[\boxed{\mathbf{3.}\mathbf{\ }}\]

\[y = x^{4} - 4x^{2} - 45\]

\[1)\ пересечение\ с\ осью\ x\]

\[y = 0:\]

\[x^{4} - 4x^{2} - 45 = 0\]

\[Пусть\ x^{2} = t \geq 0:\]

\[t^{2} - 4t - 45 = 0\]

\[D = 4 + 45 = 49\]

\[t_{1} = 2 + 7 = 9;\]

\[t_{2} = 2 - 7 = - 5\ (не\ подходит).\]

\[Подставим:\]

\[t = 9\]

\[x^{2} = 9\]

\[x = \pm 3.\]

\[Точки\ пересечения:\ \]

\[(3;0)\ и\ ( - 3;0).\]

\[2)\ пересечение\ с\ осью\ \text{y\ }(x = 0):\]

\[y = 0^{4} - 4 \cdot 0^{2} - 45 = - 45\]

\[Точка\ пересечения\ (0;\ - 45).\]

\[\boxed{\mathbf{4.}\mathbf{\ }}\]

\[\frac{2x - 10}{x^{2} - 3x} - \frac{x + 4}{x^{2} + 3x} = \frac{2}{9 - x^{2}}\]

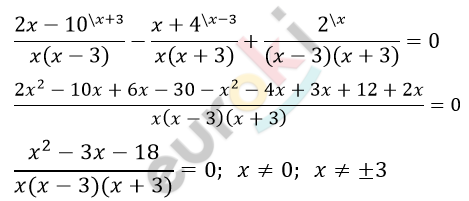
\[x^{2} - 3x - 18 = 0\]

\[x_{1} + x_{2} = 3;\ \ \ x_{1} \cdot x_{2} = - 18\]

\[x_{1} = 6;\ \ x_{2} = - 3\ (не\ подходит).\]

\[Ответ:\ x = 6.\]

\[\boxed{\mathbf{5.}\mathbf{\ }}\]

\[y = \frac{x^{3}}{x - 1}\ \ и\ \ y = x^{2} + 3x - 2\]

\[\frac{x^{3}}{x - 1} = x^{2} + 3x - 2\]

\[- 2x^{2} + 5x - 2 = 0\ \ \ \ \ | \cdot ( - 1)\]

\[2x^{2} - 5x + 2 = 0\]

\[D = 25 - 16 = 9\]

\[x_{1} = \frac{5 + 3}{4} = 2;\ \ \]

\[x_{2} = \frac{5 - 3}{4} = 0,5\]

\[y_{1} = 4 + 6 - 2 = 8;\]

\[y_{2} = 0,25 + 1,5 - 2 = - 0,25\]

\[Координаты\ точек\ \ \]

\[пересечения\ графиков:\]

\[(2;8)\ и\ (0,5;\ - 0,25).\]

## КР-4. Неравенства с одной переменной