Решебник по алгебре 9 класс Макарычев контрольные работы КР-2. Квадратичная функция и ее график. Степенная функция. Корень n-й степени Вариант 1

Условие:

1. Постройте график функции y = x² – 6x + 8. Найдите по графику:

а) значения x, при которых функция принимает отрицательные значения;

б) промежутки возрастания функции.

2. Не выполняя построения, найдите координаты точек пересечения графика функции y = x² – 8x + 12:

а) с осью x;

б) с осью y.

3. Найдите значение выражения:

а) ∛(-64)

б) \(0,8\sqrt[5]{32}\)

4. Не выполняя построения, определите, пересекаются ли графики функций

y = 3x² – 1 и y = 2x + 20. При положительном ответе укажите координаты точек пересечения.

\[1,5\sqrt[5]{- 243} + 0,6\sqrt[3]{- 2\frac{10}{27}}\]

\[\boxed{\mathbf{1.}\mathbf{\ }}\]

\[y = x^{2} - 6x + 8 =\]

\[= x^{2} - 6x + 9 - 1 =\]

\[= (x - 3)^{2} - 1\]

\[Перенесем\ график\ y = x^{2}\ \]

\[на\ 3\ ед.\ вправо\ и\ на\ 1\ ед.\ вниз:\]

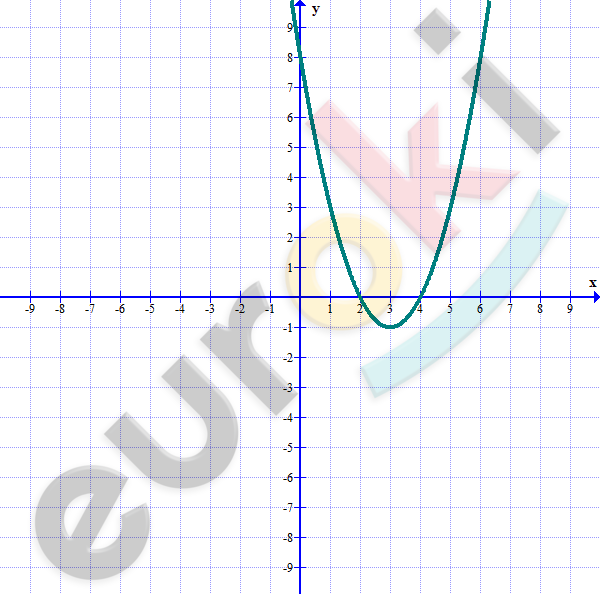
\[\textbf{а)}\ y < 0\ при\ x \in (2;4).\]

\[\textbf{б)}\ Функция\ возрастает\ на\ \]

\[промежутке:\ x \in (3; + \infty).\]

\[\boxed{\mathbf{2.}\mathbf{\ }}\]

\[y = x^{2} - 8x + 12\]

\[\textbf{а)}\ с\ осью\ \text{x\ }(y = 0):\]

\[x^{2} - 8x + 12 = 0\]

\[D = 16 - 12 = 4\]

\[x_{1} = 4 + 2 = 6;\ \]

\[x_{2} = 4 - 2 = 2\]

\[Точки\ пересечения\ (6;0);(2;0).\]

\[\textbf{б)}\ с\ осью\ \text{y\ }(x = 0).\]

\[y = 0 - 8 \cdot 0 + 12 = 12\]

\[Точка\ пересечения\ (0;12).\]

\[\boxed{\mathbf{3.}\mathbf{\ }}\]

\[\textbf{а)}\ \sqrt[3]{- 64} = - 4\]

\[\textbf{б)}\ 0,8\sqrt[5]{32} = 0,8 \cdot 2 = 1,6\]

\[\boxed{\mathbf{4.}\mathbf{\ }}\]

\[y = 3x^{2} - 1\ \ и\ y = 2x + 20\]

\[3x^{2} - 1 = 2x + 20\]

\[3x^{2} - 1 - 2x - 20 = 0\]

\[3x^{2} - 2x - 21 = 0\]

\[D = 1 + 63 = 64\]

\[x_{1} = \frac{1 + 8}{3} = \frac{9}{3} = 3;\]

\[x_{2} = \frac{1 - 8}{3} = - \frac{7}{3} = - 2\frac{1}{3}.\]

\[y_{1} = 2x + 20 = 2 \cdot 3 + 20 = 26;\]

\[y_{2} = 2 \cdot \left( - \frac{7}{3} \right) + 20 =\]

\[= - \frac{14}{3} + 20 = - 4\frac{2}{3} + 20 = 15\frac{1}{3}\]

\[Координаты\ точек\ \]

\[пересечения\ графиков:\]

\[(3;26)\ и\ \left( - 2\frac{1}{3};15\frac{1}{3} \right).\]

\[\boxed{\mathbf{5.}\mathbf{\ }}\]

\[1,5\sqrt[5]{- 243} + 0,6\sqrt[3]{- 2\frac{10}{27}} =\]

\[= 1,5 \cdot ( - 3) + 0,6\sqrt[3]{- \frac{64}{27}} =\]

\[= - 4,5 + 0,6 \cdot \left( - \frac{4}{3} \right) =\]

\[= - 4,25 - 0,8 = - 5,05\]