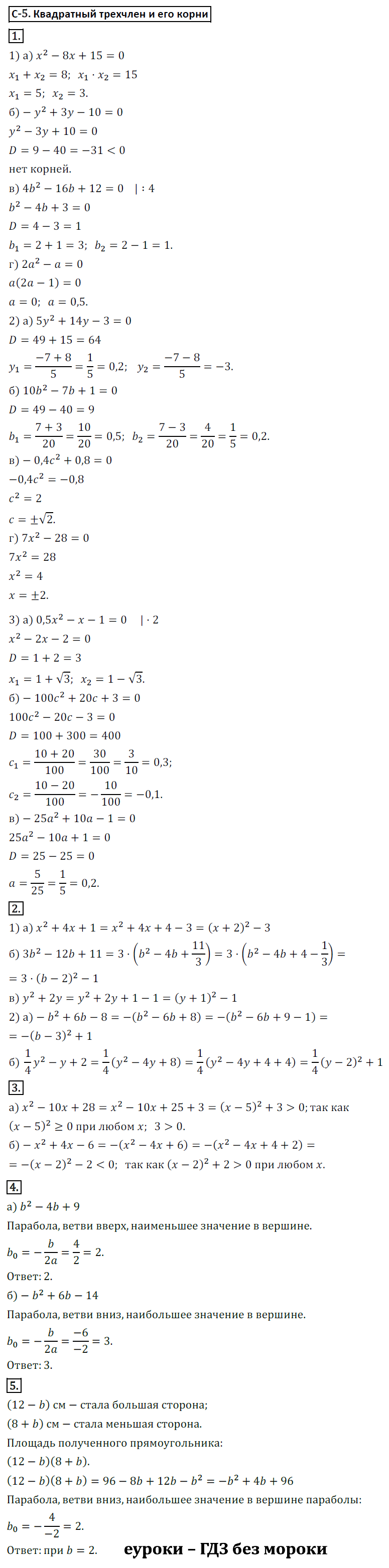Решебник по алгебре 9 класс Макарычев дидактические материалы С-5. Квадратный трехчлен и его корни | Номер Вариант 2

Условие:

1. Найдите корни квадратного трехчлена:

1) а) x^2-8x+15;

2) а) 5y^2+14y-3;

3) а) 0,5x^2-x-1.

2. Выделите квадрат двучлена из квадратного трехчлена:

1) а) x^2+4x+1;

2) а) –b^2+6b-8.

3. Докажите, что при любом x квадратный трехчлен:

а) x^2-10x+28 принимает положительные значения.

4. При каком значении b квадратный трехчлен:

а) b^2-4b+9 принимает наименьшее значение?

5. Имеется прямоугольник со сторонами 8 и 12 см. Большую его сторону уменьшили на b см, а меньшую увеличили на столько же. При каком значении b площадь полученного прямоугольника окажется наибольшей?