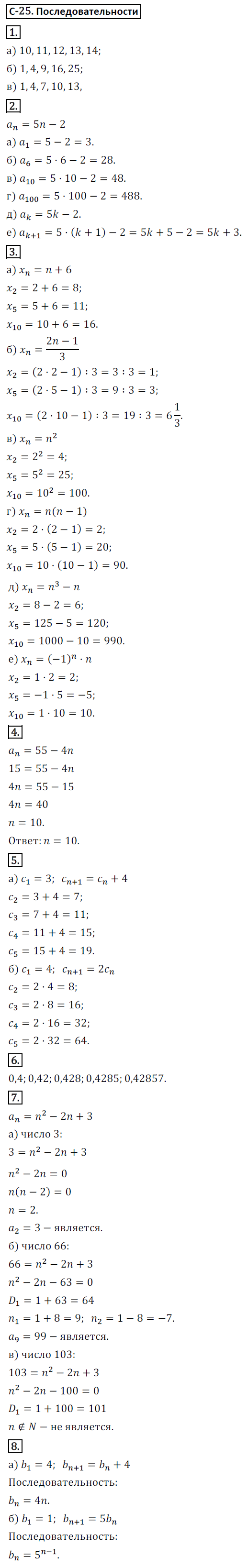Решебник по алгебре 9 класс Макарычев дидактические материалы С-25. Последовательности | Номер Вариант 1

Условие:

1. Выпишите первые пять членов последовательности:

а) двузначных чисел, взятых в порядке возрастания;

б) квадратов натуральных чисел, взятых в порядке возрастания;

в) натуральных чисел, дающих при делении на 3 остаток 1, взятых в порядке возрастания.

2. Последовательность (a_n) задана формулой a_n=5n-2. Найдите: а) a₁; б) a₆;

в) a₁₀; г) a₁₀₀; д) a_k; е) a_k+1.

3. Найдите второй, пятый и десятый члены последовательности (x_n), заданной формулой:

а) x_n=n+6.

4. Последовательность задана формулой a_n=55-4n. Найдите номер члена последовательности, равного 15.

5. Выпишите первые пять членов последовательности (c_n), если:

а) c₁=3, c_n+1=c_n+4.

6. Выпишите первые пять членов последовательности десятичных приближений с недостатком числа 3/7, взятых с точностью до 0,1: 0,01; 0,001 и т. д.

7. Последовательность (a_n) задана формулой a_n=n^2-2n+3. Является ли членом последовательности число: а) 3; б) 66; в) 103?

8. Задайте формулой n-го члена последовательность (b_n), если:

а) b₁=4, b_n+1=b_n+4.