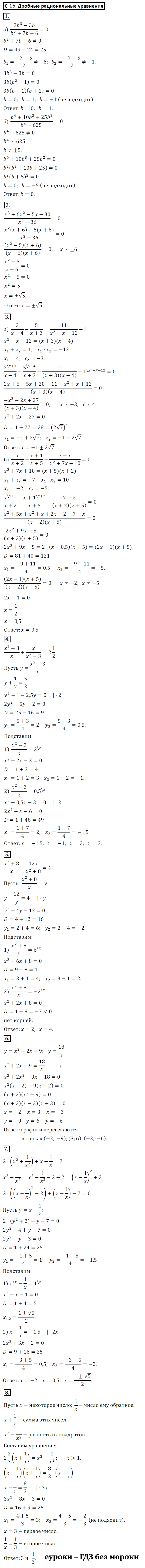Решебник по алгебре 9 класс Макарычев дидактические материалы С-15. Дробные рациональные уравнения | Номер Вариант 2

Условие:

1. При каких значениях b равно нулю значение дроби:

а) (3b^3-3b)/(b^2+7b+6).

2. Решите уравнение

(x^3+6x^2-5x-30)/(x^2-36)=0.

3. Найдите корни уравнения:

а) 2/(x-4)-5/(x+3)=11/(x^2-x-12)+1.

4. Решите уравнение, обозначив одну из взаимно обратных дробей через t, а другую – через 1/t:

(x^2-3)/x+x/(x^2-3)=2 1/2.

5. Решите уравнение, используя введение новой переменной:

(x^2+8)/x-(12x)/(x^2+8)=4.

6. Не выполняя построения, найдите координаты точек пересечения графиков функций y=x^2+2x-9 и y=18/x.

7. Найдите корни уравнения

2(x^2+1/x^2)+x-1/x=7.

8. Сумма некоторого числа, большего 1, и числа, ему обратного, в 2 2/3 раза меньше разности их квадратов. Найдите эти числа.