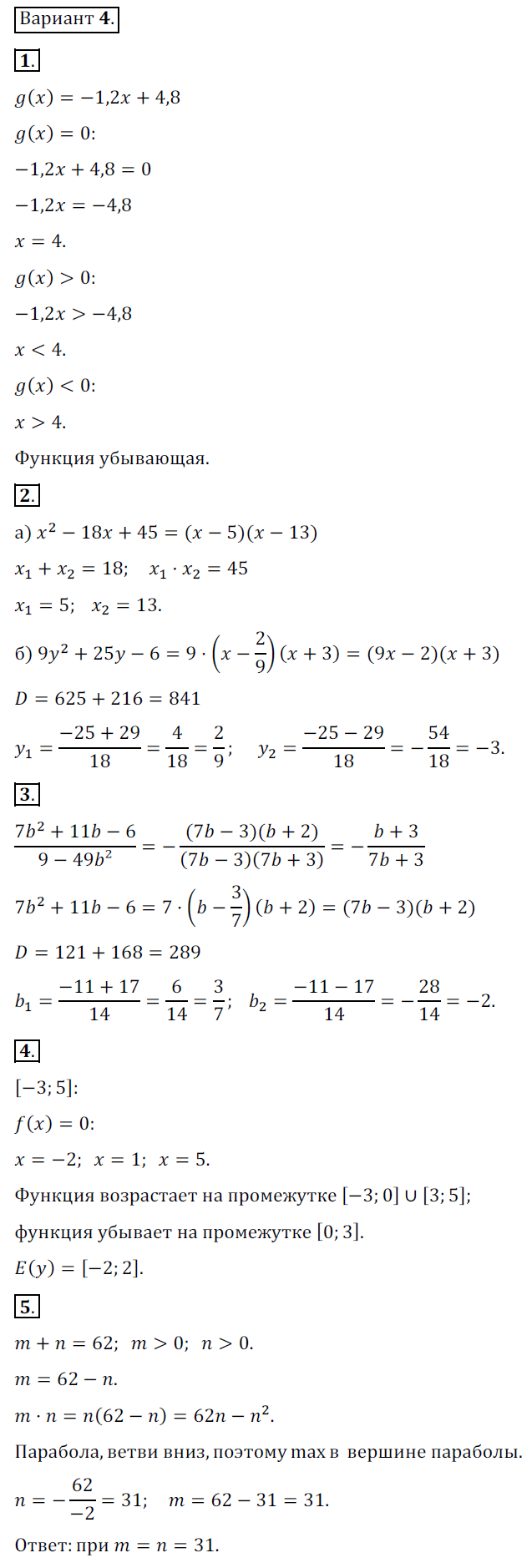Решебник по алгебре 9 класс Макарычев дидактические материалы К-1. Параграф 1. Функции и их свойства. Параграф 2. Квадратный трёхчлен | Номер Вариант 4

Условие:

1. Дана функция g(x)=–1,2x+4,8. При каких значениях аргумента g(x)=0,

g(x)<0, g(x)>0? Является ли эта функция возрастающей или убывающей?

2. Разложите на множители квадратный трехчлен

а) x^2-18x+45;

б) 9y^2+25y-6.

3. Сократите дробь

(7b^2+11b-6)/(9-49b^2).

4. Область определения функции g (рис. 20) — отрезок [–3; 5]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.

5. Сумма положительных чисел m и n равна 62. При каких значениях m и n их произведение будет наибольшим?