Решебник по математике 8 класс. вероятность и статистика Высоцкий ФГОС Часть 2 Задание 241

\[\boxed{\mathbf{241.}}\]

\[p = \frac{2}{3};\ \ q = \frac{1}{3}.\]

\[\textbf{а)}\ C_{5}^{2} \cdot \left( \frac{2}{3} \right)^{2} \cdot \left( \frac{1}{3} \right)^{3} =\]

\[= \frac{5!}{2!3!} \cdot \frac{4}{9} \cdot \frac{1}{27} = \frac{4 \cdot 5 \cdot 4}{2 \cdot 243} =\]

\[= \frac{40}{243} \approx 0,165.\]

\[\textbf{б)}\ C_{5}^{1} \cdot \frac{2}{3} \cdot \left( \frac{1}{3} \right)^{4} = \frac{5 \cdot 2}{3^{5}} =\]

\[= \frac{10}{243} \approx 0,041.\]

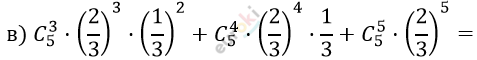
\[= \frac{5!}{3!2!} \cdot \frac{8}{243} + 5 \cdot \frac{16}{243} + \frac{32}{243} =\]

\[= \frac{80}{243} + \frac{80}{243} + \frac{32}{243} =\]

\[= \frac{192}{243} \approx 0,79.\]

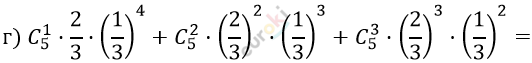
\[= 5 \cdot \frac{2}{3^{5}} + 2 \cdot 5 \cdot \frac{4}{3^{5}} + 2 \cdot 5 \cdot \frac{8}{3^{5}} =\]

\[= \frac{10}{243} + \frac{40}{243} + \frac{80}{243} =\]

\[= \frac{130}{243} \approx 0,535.\]