Решебник по алгебре 8 класс Мерзляк ФГОС Задание 865

\[\boxed{\mathbf{865\ (865).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[4x^{2} + \frac{1}{x^{2}} = 6\]

\[4x^{2} - 4x \cdot \frac{1}{x} + \frac{1}{x^{2}} + 4 = 6\]

\[\left( 2x - \frac{1}{x} \right)^{2} = 2\]

\[2x - \frac{1}{x} = \pm \sqrt{2}\]

\[\boxed{\mathbf{8}\mathbf{6}\mathbf{5}\mathbf{\text{.\ }}Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Расположим\ кусочки\ в\ порядке\ \]

\[увеличения\ массы:\]

\[m < m_{2} < \ldots < m_{9}.\]

\[В\ одну\ тарелку\ положили\ \]

\[m_{1},\ m_{3},\ m_{5},\ m_{7},\ \]

\[а\ в\ другую - m_{2},\ m_{4},\ m_{6},\ m_{8}.\]

\[а\ если\ в\ первую\ тарелку\ \]

\[положить\ m_{9},\ то\ \]

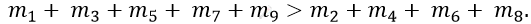
\[Следовательно,\ можно\ \]

\[разрезать\ m_{9}.\]

\[Ответ:можно.\]