Решебник по алгебре 8 класс Мерзляк ФГОС Задание 851

 

\[\boxed{\mathbf{851\ (851).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[\frac{a - b - a + c + b - c}{(b - c)(c - a)(a - b)} = 0\]

\[\frac{0}{(b - c)(c - a)(a - b)} = 0\]

\[0 = 0.\]

\[\boxed{\mathbf{8}\mathbf{5}\mathbf{1}\mathbf{\text{.\ }}Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x\ ч - время\ заполнения\ \]

\[через\ первую\ трубу,\ \]

\[а(x + 2)\ ч - через\ вторую\ \]

\[трубу\ и\ (x + 8)\ ч - через\ \]

\[третью.\]

\[По\ условию\ известно,\ что\ для\ \]

\[наполнения\ бассейна\ через\ \]

\[первую\ трубу\ надо\ столько\ \]

\[времени,\ как\ для\ наполнения\ \]

\[через\ вторую\ и\ третью\ вместе.\]

\[Составляем\ уравнение:\]

\[\frac{1}{x} = \frac{1}{x + 2} + \frac{1}{x + 8}\]

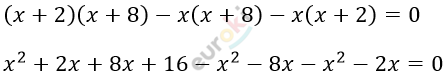
\[- x^{2} + 16 = 0\]

\[x^{2} = 16\]

\[x = 4\ (ч) - через\ первую\ трубу.\]

\[x = - 4 \Longrightarrow не\ удовлетворяет\ \]

\[условию.\]

\[4 + 2 = 6\ (ч) - через\ вторую\ \]

\[трубу.\]

\[4 + 8 = 12\ (ч) - через\ третью\ \]

\[трубу.\]

\[Ответ:4\ ч,\ 6\ ч,\ 12\ ч.\]