Решебник по алгебре 8 класс Мерзляк ФГОС Задание 804

 

\[\boxed{\mathbf{804\ (804).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[автомобиля,\ а\ скорость\ \]

\[автобуса\ (x - 20)\ \frac{км}{ч}.Тогда\ \]

\[автомобиль\ проезжает\ \]

\[расстояние\ за\ \frac{240}{x}\ ч,\ \]

\[а\ автобус - за\ \ \frac{240}{x - 20}\ ч.\]

\[По\ условию\ известно,\ \]

\[что\ автобус\ приехал\ на\ 1\ час\ \]

\[позже.\]

\[Составляем\ уравнение:\]

\[\frac{240}{x} - \frac{240}{x - 20} + 1 = 0;\ \ \ \ \ \ x \neq 0;\ \ \ \ \]

\[x \neq 20\]

\[x^{2} - 20x - 4800 = 0\]

\[D = 400 + 19\ 200 = 19\ 600\]

\[x = \frac{20 + 140}{2} = 80\ \left( \frac{км}{ч} \right) -\]

\[скорость\ автомобиля.\]

\[x = \frac{20 - 140}{2} = - 60 \Longrightarrow не\ \]

\[удовлетворяет\ условию.\]

\[80 - 20 = 60\ \left( \frac{км}{ч} \right) -\]

\[скорость\ автобуса.\]

\[Ответ:80\ \frac{км}{ч};60\ \frac{км}{ч}.\]

\[\boxed{\mathbf{80}\mathbf{4}\mathbf{\text{.\ }}Еуроки\ - \ ДЗ\ без\ мороки}\]

\[1)\left( a^{2} - a - 6 \right)x = a² - 9\]

\[a^{2} - a - 6 = 0\]

\[a_{1} + a_{2} = 1,\ \ a_{1} = - 2\]

\[a_{1} \cdot a_{2} = - 6,\ \ a_{2} = 3\]

\[(a + 2)(a - 3)x = (a - 3)(a + 3)\]

\[x = \frac{(a - 3)(a + 3)}{(a - 3)(a + 2)}\]

\[x = \frac{a + 3}{a + 2}\]

\[если\ a = 3,\ \ \ \]

\[то\ x - любое\ число;\]

\[если\ a = - 2,\ \ \ то\ корней\ нет;\]

\[если\ a \neq 3\ \ и\ \ \ a \neq - 2,\ \ \ \]

\[то\ x = \frac{a + 3}{a + 2}.\]

\[2)\ \left( a^{2} - 8a + 7 \right)x =\]

\[= 2a² - 13a - 7\]

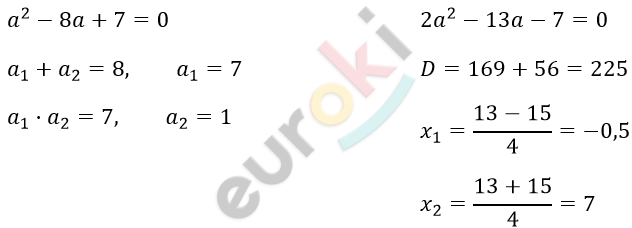
\[(a - 7)(a - 1)x =\]

\[= 2 \cdot (a - 7)(a + 0,5)\]

\[x = \frac{2 \cdot (a - 7)(a + 0,5)}{(a - 7)(a - 1)}\]

\[x = \frac{2 \cdot (a + 0,5)}{a - 1}\]

\[\ если\ a = 7,\ \ \ x - любое\ число.\]

\[если\ a = 1,\ \ \ \ корней\ нет.\]

\[если\ a \neq 1\ \ \ и\ \ a \neq 7,\ \ \ \]

\[то\ x = \frac{2 \cdot (a + 0,5)}{a - 1}.\]