Решебник по алгебре 8 класс Мерзляк ФГОС Задание 612
Задание 612



\[\boxed{\mathbf{612\ (612).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[1)\frac{1}{a^{2} - 4b^{2}}\ :\frac{a + 2b}{(2b - a)^{2}} =\]
\[= \frac{(2b - a)^{2}}{(a - 2b)(a + 2b)(a + 2b)} =\]
\[= \frac{a - 2b}{(a + 2b)^{2}}\]
\[2)\ \frac{a - 2b}{a(a + 2b)} - \frac{a - 2b}{(a + 2b)^{2}} =\]
\[= \frac{a^{2} - 4b^{2} - a^{2} + 2ab}{a(a + 2b)^{2}} =\]
\[= \frac{- 4b^{2} + 2ab}{a(a + 2b)^{2}}\]

\[\frac{2b}{a^{2}} = \frac{2b}{a^{2}} \Longrightarrow что\ и\ требовалось\ \]
\[доказать.\]

\[1)\ \frac{2a}{a + 3} - \frac{4a}{(a + 3)^{2}} =\]
\[= \frac{2a^{2} + 6a - 4a}{(a + 3)^{2}} = \frac{2a(a + 1)}{(a + 3)^{2}}\]
\[2)\frac{2a(a + 1)}{(a + 3)^{2}} \cdot \frac{(a - 3)(a + 3)}{a + 1} =\]
\[= \frac{2a(a + 1)(a - 3)(a + 3)}{(a + 3)^{2}(a + 1)} =\]
\[= \frac{2a(a - 3)}{a + 3}\]
\[3)\ \frac{2a^{2} - 6a}{a + 3} - \frac{a^{2} - 9a}{a + 3} =\]
\[= \frac{2a^{2} - 6a - a^{2} + 9a}{a + 3} =\]
\[= \frac{a(a + 3)}{(a + 3)} = a\ \ \ \]
\[a = a \Longrightarrow что\ и\ требовалось\ \]
\[доказать.\]

\[\boxed{\mathbf{61}\mathbf{2}\mathbf{\text{.\ }}Еуроки\ - \ ДЗ\ без\ мороки}\]
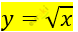
\[1)\ A\ (16;4):\ \]
\[4 = \sqrt{16}\ \]
\[4 = 4 \Longrightarrow \ \ график\ проходит\ \]
\[через\ ( \cdot )A.\]
\[2)\ \text{B\ }(49;\ - 7):\ \ \]
\[- 7 \neq \sqrt{49}\text{\ \ }\]
\[- 7 \neq 7 \Longrightarrow \ \ не\ проходит\]
\[через\ ( \cdot )B.\]
\[3)\ \text{C\ }(3,6;0,6):\ \ \]
\[0,6 \neq \sqrt{3,6} \Longrightarrow \ график\ \]
\[не\ проходит\ через\ ( \cdot )C.\]
\[4)\ \text{D\ }( - 36;6):\ \ \]
\[6 \neq - \sqrt{36} \Longrightarrow \ \ \ график\ \]
\[не\ проходит\ через\ ( \cdot )D.\]





