Решебник по алгебре 8 класс Мерзляк ФГОС Задание 372

 

\[\boxed{\text{372\ (372).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[S = a^{2} - площадь\ квадрата.\]

\[1)\ a^{2} = 25\]

\[a = 5\ \]

\[a = - 5 - не\ может\ быть\ \]

\[сторона\ квадрата\ \]

\[отрицательным\ числом.\]

\[Ответ:a = 5\ см.\]

\[2)\ a^{2} = 1600\]

\[a = 40\]

\[a = - 40 - невозможно.\]

\[Ответ:a = 40\ дм.\]

\[3)\ 0,04 = a^{2}\]

\[a = 0,2\]

\[a = - 0,2 - невозможно.\]

\[Ответ:a = 0,2\ м.\]

\[\boxed{\text{372.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

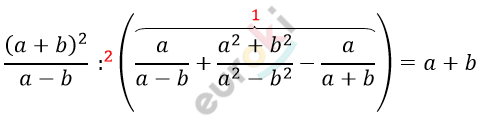
\[Преобразуем\ левую\ часть\ равенства\ (по\ действиям):\]

\[1)\frac{a^{\backslash a + b}}{a - b} + \frac{a^{2} + b^{2}}{a^{2} - b^{2}} - \frac{a^{\backslash a - b}}{a + b} =\]

\[= \frac{a(a + b) + a^{2} + b^{2} - a(a - b)}{(a - b)(a + b)} =\]

\[= \frac{a^{2} + ab + a^{2} + b^{2} - a^{2} + ab}{(a - b)(a + b)} =\]

\[= \frac{a^{2} + 2ab + b^{2}}{(a - b)(a + b)} =\]

\[= \frac{(a + b)^{2}}{(a - b)(a + b)} = \frac{a + b}{a - b}\]

\[2)\ \frac{(a + b)^{2}}{a - b}\ :\ \frac{a + b}{a - b} =\]

\[= \frac{(a + b)^{2} \cdot (a - b)}{(a - b)(a + b)} = a + b\]

\[a + b = a + b\]

\[Что\ и\ требовалось\ доказать.\]