Решебник по алгебре 8 класс Мерзляк ФГОС Задание 347

 

\[\boxed{\text{347\ (347).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ \text{x\ }монет\ получил\ первый\ \]

\[мужчина,\ тогда\ y\ монет\ \]

\[получил\ второй\ мужчина.\]

\[\ Значит,\ x + \frac{y}{2} =\]

\[= 48\ монет\ и\ y + \frac{2}{3}x =\]

\[= 48\ монет.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} x + \frac{y}{2} = 48\ \ \ \\ y + \frac{2}{3}x = 48 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} x = 48 - \frac{y}{2}\text{\ \ } \\ y + \frac{2}{3}x = 48 \\ \end{matrix} \right.\ \]

\[y + \frac{2}{3} \cdot \left( 48 - \frac{y}{2} \right) = 48\]

\[y + 32 - \frac{y}{3} - 48 = 0\]

\[y - \frac{y}{3} - 16 = 0\ \ \ \ \ \ \ | \cdot 3\]

\[3y - y - 48 = 0\]

\[2y - 48 = 0\]

\[y = 24\ (монеты) - \ получил\ \]

\[второй\ мужчина.\]

\[x = 48 - \frac{24}{2} = 48 - 12 =\]

\[= 36\ (монет) - \ получил\ \]

\[первый\ мужчина.\]

\[Ответ:36\ монет\ и\ 24\ монеты.\]

\[\boxed{\text{347.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

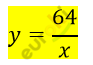
\[так\ как\ x = y:\]

\[x = \frac{64}{x}\]

\[x^{\backslash x} - \frac{64}{x} = 0\]

\[\frac{x^{2} - 64}{x} = 0\]

\[\left\{ \begin{matrix} x^{2} - 64 = 0 \\ x \neq 0\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\left\{ \begin{matrix} x = 8\ \ \ \\ x = - 8 \\ x \neq 0\ \ \ \\ \end{matrix} \right.\ \]

\[\text{A\ }(8;8);\ \ B\ ( - 8;\ - 8)\]

\[Ответ:\ A\ (8;8);\ \ B\ ( - 8;\ - 8).\]